アウトカム　outcome

アウトカムとは，転帰と訳され，治療や予防などの医学的介入から得られるすべての結末のことです．臨床研究においては，介入効果によって得られる判定項目をアウトカムといいます．
EBPTにおけるアウトカムには，包括的健康関連QOLの評価，ADLなど総合的な活動レベルの評価，歩行など要素的な活動レベルの評価，筋力や関節可動域など機能・構造レベルの評価があげられます．EBPTを実践する時には，個々の患者によって重要となるアウトカムは異なるので，改善すべき症状を決定したうえで適切に選択することが必要となります．たとえば，関節可動域の測定結果は改善しているにも関わらず，疼痛やADLの指標に改善が見られないケースがあります．

ROC曲線　 receiver operating characteristic curve

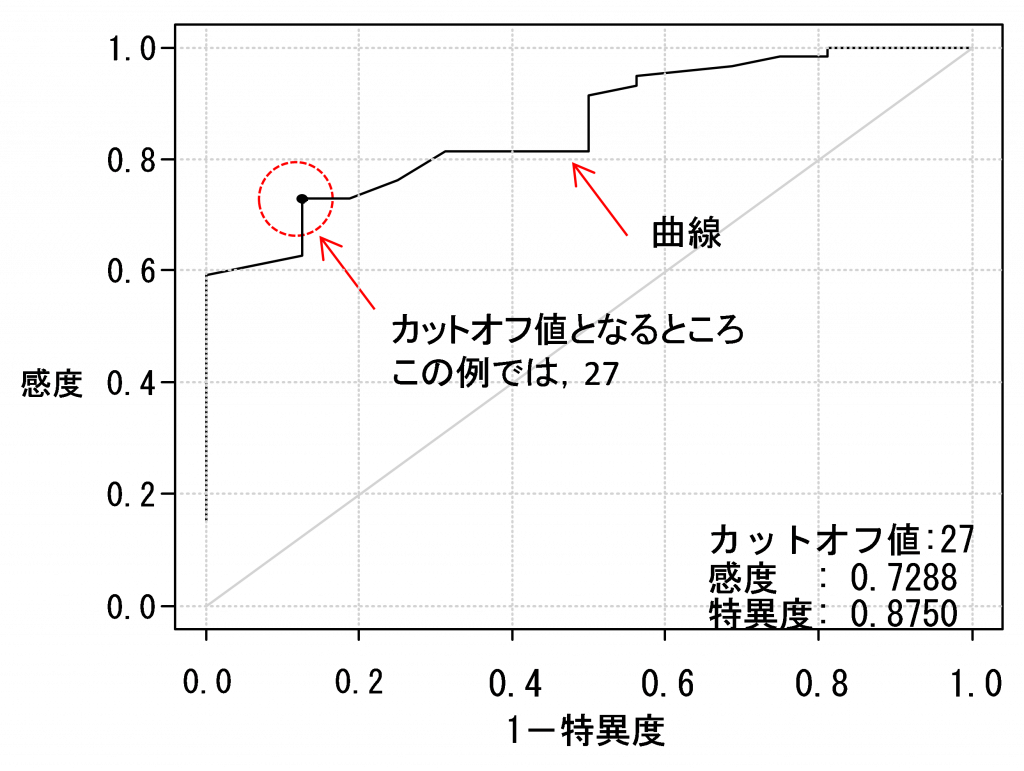
ある検査の感度と特異度の関係を曲線（または折れ線）で表したグラフです．縦軸に感度，横軸に（1－特異度）をとり，検査の値を変化させた際の感度と（1－特異度）を表示し，曲線で表します．曲線がグラフ左上の角に近い位置にあるほど感度と特異度が優れていることになります．一般的に左上の角に近い検査値のところを，最適なカットオフ値とします．

アドヒアランス　adherence

　遵守またはコンプライアンス(compliance)のこと．被験者が実施することになっている研究プログラムを，どの程度実行したのかを示します．または，研究者が，研究プログラムの全過程において，必要な検査測定や介入などを実施する上で，被験者の適切な管理をどの程度実行したかを示します．

アルゴリズム　algorithm

　ある特定の状況や問題に適用できる選択肢の中から，適切なものをたどって手順を行っていけば，その問題を解決することができるような論理構成となっています．
例えば，「骨折しているかを調べるのであれば，レントゲンを撮影する」，「大腿骨頸部骨折でGarden分類IVであれば，人工骨頭置換術を行う」など，「AであればBを行う」という流れでできています．

異質性の検定　test for heterogeneity

　複数の研究を統合するメタ分析などでは，研究間の結果にばらつきがあるかどうかを異質性の検定を用いて確認します．Cochran Q testではp値が5%より小さい場合，ばらつきの程度を％で表すI²検定では50%より大きい場合に，異質性がかなり高いと判断します．これらの検定結果は，異質性を視覚的に判断することができるフォレストプロットとともに示されることが一般的です．メタ分析で示された統合値を確認する時には，採用された研究間の異質性が低いかどうかに着目する必要があります．

1元配置分散分析　one-way analysis of variance（one-way ANOVA）

　3群以上のデータ（対応のないデータ）に対して，平均の差を検定する手法です．これらの群は，疾患別｛健常群，患者A群，患者B群，…｝とか，介入別｛運動療法群，物理療法群，非介入群，…｝などの，あるルールに従って分けられています．分散分析では，この疾患別，介入別といったルールを「要因」と呼びます．要因が特に1つある場合を，1元配置分散分析といいます．
　たとえば，健常群，変形性股関節症群，変形性膝関節症群において，膝関節伸展筋力の差を検定するときに用いられます．この群の分け方は疾患別といった1つの要因で分けられるので，1元配置分散分析の適用となります．検定の結果，有意に差が認められた場合，「疾患別の要因で有意に差があった」とか「有意な主効果が認められた」などと記述します．しかし，分散分析では，あくまで3群間全体の要因に差があるかどうかを検定する手法であるため，どの群間に差があるかを検定するためには，この後に多重比較法を行います．

一次資料　primary source

原著論文を意味します．原著論文とは，論文の最も基本的なものです．研究を行った人自身が，自分たちの研究方法や結果を示しながら考察を行い，その上で著者として独自の結論を出すものです．一次資料は大きく「臨床研究」と「基礎研究」の2種類に分けられます．「臨床研究」とは，実際の患者を対象として行われる研究です．それらの結果は，我々が患者に対して数ある治療法の中から最も望ましいものを選択する際などに使われます．「基礎研究」とは，基礎医学的な手法を行う研究のことを表します．この結果が直接臨床場面に活かされることは少ないですが，基礎研究の積み重ねやその応用によって新たな治療方法が見出されることがあります．

一般線型モデル　general linear model（GLM）

　一般的に使われている統計的手法である，正規分布を仮定した検定や解析，つまりt検定（差の検定としての），F検定，分散分析，重回帰分析などの手法全体を一般線型モデルと呼びます．
　従来は，t検定や分散分析や重回帰分析は，別々の呼び名で呼んでいましたが，数理的な特徴を紐解くと，全て共通の理論で成立していることがわかっています．このことを踏まえて，最近では統一して，一般線型モデルと呼ぶ傾向になってきています．しかし，まだ普及している用語とは言い難いため，未だ統計的手法を区別して呼ぶ場合が大半です．
　正規分布を仮定しないロジスティック回帰分析やコックス比例ハザードモデルは別のものとして，一般化線形モデル（generalized linear model；GLM）と呼ばれます．通常，ＧＬＭと略する場合は，この一般化線型モデルを指すことが多いのですが，統一された見解はありません．

EBPT　evidence-based physical therapy

理学療法の臨床活動において，評価や治療の方法などを選択することを臨床判断（clinical decision making）といいます．このような理学療法士による臨床判断を“経験則”だけに基づいて行うのではなく，①基本的な理論，②理学療法士の臨床能力や臨床経験，③患者さんの意向や価値観とともに，④質の高い臨床研究による検証結果であるエビデンス（evidence）“も”含めて行うことによって，患者さんの臨床状況に即した安全で効果的な理学療法を実践するための行動様式のことを“根拠に基づいた理学療法（Evidence-based Physical Therapy，EBPT）”と呼びます．EBPTの進め方は，①患者に関する臨床的疑問（クリニカルクエスチョン）の定式化，②患者の臨床的疑問に関連した情報の検索・収集，③収集した情報の批判的吟味，④批判的吟味を行った情報の患者への適用の検討，⑤実施したEBPTプロセスの評価という5段階のステップとなります．多忙な臨床現場で効率よくEBPTを実践するためには，この5つのステップの進め方を正しく理解するとともに，このEBPT用語集にリストアップされたような臨床疫学的な概念や研究方法論についての理解を深めていくことが大切です．

イベント　event

疾患や症状の発症，入院，死亡などの有害な事象が対象者に発生することをいいます．臨床試験の報告内容を定めた国際的な統合基準であるコンソート声明では，研究中に有害なイベントが発生した場合には，その内容を論文に記載するようにと記載されています．また，対象者のうちイベントが確認された割合のことをイベント発生率と呼びます．介入研究の場合には，介入の効果を検証するとともに，介入によって有害なイベントが発生しないかどうかも重要な結果となります．

因果関係　causation

　原因と結果の関係があることを因果関係といいます．因果関係を意味する英語表記は，causal association，causal relation，causal nexus，causal connection，causal sequence，causal dependence，cause-effect relationshipなど，さまざま存在しています．
　因果関係を判定する条件として，米国公衆衛生局長諮問委員会の5基準（1964）が提唱されています．
1.Consistency（一致性）：異なる地域・時代・状況でも同一のことが起こる
2.Strength（強固性）：原因と結果の関連が強い
3.Specificity（特異性）：原因と結果の間に特定の対応関係がある（原因が変われば結果も変わる）
4.Temporality（時間性）：原因が結果よりも時間的に先行する
5.Coherence（整合性）：既知の知識体系と矛盾しない
　これら5基準に，さらに以下の4条件を加えたBradford Hillの判定基準（1965）もあります．
6.Biological gradient（生物学的用量反応勾配）：定量的な反応が起こる（量－反応関係）
7.Plausibility（尤もらしさ）：生物学的に矛盾なく説明できる
8.Experiment（実験的証拠）：関連を支持する実験的研究が存在する
9.Analogy（類似性）：既存の類似した関連により裏付けられる
　以上の条件は必ずしもすべて満たす必要はありませんが，合致する条件が多くなるほど因果関係の確実性が高くなります．
　回帰分析，重回帰分析，ロジスティック回帰分析といった統計解析では，説明変数（独立変数）を原因，目的変数（従属変数）を結果とみなした因果関係を仮定しています．類似した手法に相関がありますが，相関は因果関係を仮定せずに変数間の関連度を表すものです．
注意を要するのは，回帰分析や重回帰分析，ロジスティック回帰分析を行って有意な結果を得たからといって，必ずしも実際に因果関係が成立しているわけではないという点です．有意な結果が得られた場合は，上述した5ないし9基準のStrength（強固性）を支持する形にはなりますが，他の基準について矛盾しないかどうか，といった確認も重要となります．また，原因と結果の関係が逆転するとか，交絡因子が存在する可能性もありますので，因果関係の解釈は十分慎重に行う必要があります．

因子分析　factor analysis

　複数の変数から似通った変数をまとめて，変数の小グループ（因子）を作っていく手法です．相関係数を利用して，似通った変数には高い得点（因子負荷量）を与え，各因子で因子負荷量が高い変数を分けていきます．主成分分析と非常に似ているので同様の解析と思ってもらっても差し支えありません．異なるのは，主成分分析が似通った変数をできるだけ多くまとめるのに対して，因子分析は似通っていない変数を出来るだけ分ける，という意味合いの違いがあります．
　たとえば，体力測定を行い，身長，体重，握力，背筋力，垂直跳び，走り幅跳びのデータを群分けしたいときに，因子負荷量の大きさで変数を分けていきます．仮に，第1因子で握力＞体重＞背筋力＞身長＞垂直跳び＞走り幅跳びの順に因子負荷量が高いとします．そこで身長，垂直跳び，走り幅跳びでは，第2因子の方が，因子負荷量が大きければ，第2因子と考えたほうが妥当かもしれないので，第1因子は握力，体重，背筋力で力の因子，第2因子は身長，垂直跳び，走り幅跳びで跳躍力の因子と考えます．この因子の意味づけ（構成概念の解釈）は，解析者の主観に委ねられます．

インフォームドコンセント　informed consent

　「説明と同意」とも訳されており，研究者が参加者に対して，研究内容などについての説明を十分にした上で，参加者がその研究に参加することに口頭もしくは書面において同意すること．その説明には，リスクや利益，その他の影響についてなども含まれています．

隠蔽（コンシールメント）　concealment

対象者の割り付け作業を行う人が，対照者か介入者か，またはA治療法かB治療法かという情報を知らずに，ランダムに割り付けることです．隠蔽がされていない研究では，割り付け作業を行う人が，対照群または介入群に，より症状が重い（あるいは軽い）患者を都合良く割り振ってしまう可能性があります．このような場合，ランダム割り付けが正確に行われないことで，研究結果が選択バイアス[→バイアスを参照]の影響を受けてしまうことになります．

Wilcoxonの符号順位検定　Wilcoxon signed-rank test

対応のあるデータに対して，分布の違い（対応のあるデータどうしの中央値の差）を検定するノンパラメトリックな手法（ノンパラメトリック検定）です．データの母集団分布（度数分布）は，正規分布でも正規分布以外でも，どのような分布であっても適用できます．単にWilcoxonの検定と呼ぶときもあります．
たとえば，A～Eの5名を対象として，筋力増強運動前における膝関節伸展筋力の徒手筋力検査値を測り，筋力増強運動後に再度A～E5名の膝関節伸展筋力の徒手筋力検査値を測り，筋力増強運動前後の差を知りたいというときにWilcoxonの符号順位検定を適用させます．

ウェルチの検定　Welch test

　2標本t検定[→ｔ検定（差の検定としての）を参照]を適用する前提条件の1つに，「2群の母集団の分散が等しい」という等分散性の仮定が必要となります．従って事前に等分散性の検定（たとえばLevene検定）を行って確認し，仮に等分散性を仮定できない場合，2標本t検定の代わりにウェルチの検定を適用します．なお，解析の対象となるデータは正規分布であることも前提条件となります．

後ろ向き研究　retrospective study

一定の期間を経て後ろ向きにデータをとる，縦断研究の一つです．研究を開始する時点から，過去にさかのぼって疾患や障害を引き起こした要因（人工股関節全置換術を施行された患者における転倒など）にさらされたかどうかを調べる方法です．起こったことを振り返って確認するので，交絡因子の把握が困難ですが，研究を終えるまでに要する時間が，比較的短時間ですむことが可能です．症例対照研究などが代表的なものとなります．

エビデンス　evidence

「根拠」や「証拠」と直訳されます．EBM（evidence based medicine）におけるエビデンスの意味は，「信頼性の高い臨床研究による実証結果」です．エビデンスは，立場の違いから3つの意味を含みます．エビデンスを「つくる」という立場で使われるのが臨床試験です．また，エビデンスを「つかう」という立場では医療職，医療消費者など多様なユーザーの存在があげられます．そして，「つくる」立場と「つかう」立場をつなぐ役割として，「つたえる」という立場があります．この「つたえる」立場の一つにコクラン共同計画などのエビデンスデータベースがあげられます．さらに，エビデンスには研究デザインの種類によって相対的な水準が設定されています．統計学的な見解では，ランダム化比較試験（RCT）とメタ分析が最もバイアスが生じにくく信頼性が高いといわれています．一方，臨床的な見解では，評価・治療・予防などそれぞれのカテゴリーに応じて，臨床に汎化するためにより適した研究デザインを考慮するという必要性もあります．その時点で最も信頼できる最善のエビデンスを利用することがEBPTを実践するうえでのポイントとなります．

F検定　F test

　F分布を用いて分散比の検定を行うもので，等分散性の検定として用いられます．F分布とは統計学的な分散の比を表す標本分布です．分散分析の一部として位置づけられています．帰無仮説は「2群の母分散は等しい」であり，帰無仮説が棄却されれば「2群の母分散は等しくない」という対立仮説が採用されます．

MDC95　minimal detectable change 95

　信頼性を表す指標の1つです．MDC（最小可検変化量）は，再テストなどの繰り返し測定により得られた2つの測定値の変化量の中で測定誤差の大きさを示したもので，MDC 以内の変化は測定誤差によるもの，それ以上の変化が測定誤差以上の変化と判断されます．このMDC値の95％信頼区間がMDC95です．
　例をあげると，TUGT（Timed Up and Go test）のMDC95が2.9秒と求められた場合，同じ対象者に対して2回TUGTを行い，2.9秒以内の差であれば測定誤差によるもの，2.9秒より大きい差であれば，測定誤差以上の変化と判断されます．

エンドポイント　endpoint

エンドポイントは「終了点，終点」という意味なので，研究において観察もしくは介入を終了する点という意味になります．臨床研究では介入（治療）効果を判定する最終的な到達指標のことになります．エンドポイントは，しばしばアウトカムと同義に述べられることもあり，混同して用いられていますが，介入による全ての結果がアウトカムであり，介入効果を判定する，または観察を終了するための結果がエンドポイントとなります．したがって，エンドポイントはアウトカムに包括される（狭義のアウトカム）と考えられます．エンドポイントには真のエンドポイントと代用エンドポイントがあります．真のエンドポイントとは，最終的な観察終了点です．
転倒予防を目的として一定期間のバランストレーニングを行った研究の例をあげましょう．バランストレーニングを行って，介入前，6ヵ月間の介入終了時，介入終了から1年後の各時点で下肢の筋力，歩行速度，片脚立位保持時間，重心動揺面積，Timed Up and Go Test，転倒の発生率を測定したとします．これら全ての評価結果はアウトカムです．この研究の目的は転倒予防であるので，真のエンドポイントは介入終了から1年後における転倒の発生率となります．もし，6ヵ月間の介入終了時にバランス能力が向上した者は将来的に転倒予防効果が高いという関連があるのなら，代用エンドポイントとして6ヵ月間の介入終了時のバランス能力を表すと考えられる片脚立位保持時間や重心動揺面積が選ばれます．

黄金律（ゴールドスタンダード）　gold standard

ゴールドスタンダードとは，診断や評価の精度が高いものとして広く容認された手法のことであり，標準基準 (criterion standard)や参照基準(reference standard)ともいわれています．理学療法の臨床で新たな評価法や効果判定の方法を検討する際には，その新たな手法を，ゴールドスタンダードとなる既存の基準や評価方法と比較しなければ，新たな手法の妥当性は検証できません．
たとえば，理学療法の臨床において，肩関節周囲炎の患者が上肢を最大挙上した際に，大結節が肩峰下を通過しているかどうかについて，肩関節屈曲可動域から評価可能かどうかを検討しようと考えたとします．その場合には，複数の患者の肩関節屈曲最終域の関節可動域を測定すると同時に，その時のX線画像をゴールドスタンダードの基準として比較することで，肩関節屈曲可動域とX線画像による肩峰と大結節の位置関係について検証することになります．

横断研究　cross-sectional study

ある特定の対象に対して，疾患や障害における評価，介入効果などを，ある一時点において測定し，検討を行う研究です．過去にさかのぼったり，将来にわたって調査したりはしません．利点としては，時間的・経費的な効率が良く，いくつかの要因に着目して比較でき，様々な要因を一度に測定し，検討できるなどの点があげられます．欠点としては，バイアスの影響が入りやすく，原因と結果の因果関係が明確ではないなどの点があげられます．
たとえば，変形性膝関節症の患者に対して，ストレッチの即時効果を検討することや，糖尿病患者の30秒間立ち上がりテストで何回立ち上がることができるかを測定することといった研究デザインが考えられます．

オッズ比　odds ratio

対照（病気を持たない人）に比べて，患者のうち，どれくらいの人に，病気の原因（リスク要因）があるかを表す指標です．たとえばオッズ比が5のとき，「健常者に比較して脳卒中の人は，高血圧の要因を5倍持っている」というように用います．
患者のオッズは，患者のうちリスク要因を持つ者の割合（患者でリスク要因を持つオッズ）で表されます．他方，健常者のオッズは健常者のうちリスク要因を持つ者の割合（健常者でリスク要因を持つオッズ）で表されます．それらオッズの比，すなわち（患者でリスク要因を持つオッズ÷健常者でリスク要因を持つオッズ）により算出される値が，オッズ比です．

重みづけ平均　weighted average

　重みづけ平均とは，メタ分析にて，定量的に正しく個々の研究の効果量を統合するために，質の高いランダム化比較試験（RCT）などの研究の効果量を，そうでない研究の効果量に比べて，より重視するための統計学的方法です．固定効果モデル（メタ分析）と変量効果モデル（メタ分析）の2つの考え方があります．各研究の重みは，各研究における推定誤差の分散の逆数を求めることで計算できます．

I²統計量　I² statistics

　メタ分析において個々の研究結果の違いやばらつきがないかを確認する異質性の検定の一つであるI²検定で求められた数値のことで，フォレストプロット内に％で示されます．この値が，0～25％は異質性なし，25～50％は中等度の異質性あり，50～75％は強い異質性あり，75%以上はとても強い異質性ありと言われていますが，各論文によってとらえかたが異なっているのが現状です．異質性の検定として用いられるコクランズの統計量Q値は，研究の数や指標に左右されることに対して，I²統計量は，研究の数に影響を受けにくいといわれています．

AGREE２　the Appraisal of Guidelines for REsearch and Evaluation

　診療ガイドラインの質を評価するためのツールであり，The Appraisal of Guidelines for REsearch and Evaluationの略語です．日本語版がウェブ上にて公開されており，ガイドライン作成者・利用者などは，複製・使用してもよいとされていますが，商業目的での利用や販売促進での使用は禁じられています．評価内容としては，6領域23項目と全体評価を7段階（１：全くあてはまらない～７：強くあてはまる）で点数をつけていき，このガイドラインの使用を推奨するかどうか（推奨する，条件付きで推奨する，推奨しない）について判断します．これらの評価を行うことで，ガイドライン作成者は，点数の低い項目を改善しながら質の向上を図ることができ，ガイドライン利用者は，公開されているガイドラインの質が高いか低いかを知ることができます．ただし，目の前の患者や利用者に適したガイドラインであるかどうかは，AGREE２の点数だけでは判断できないため，利用者が考慮する必要があります．
 

エビデンスレベル　evidence level

　エビデンスヒエラルキーとも呼ばれています．主に研究デザインによるエビデンスの質によって分類される指標です．ランダム化比較試験（RCT）のメタ分析のエビデンスレベルが最も高く，観察研究や専門家の意見などは低いとされています．
 　一方，EBMを提唱したカナダのマクマスター大学のGuyattらは，質の低いランダム化比較試験（RCT）であっても質が高いと評価されたり，質の高い観察研究であっても質が低いと評価されるという問題があることから，エビデンスレベルだけで判断するのではなく，「推奨の強さ」と「エビデンスの確実性」という両面から複数の研究を統合した重要なアウトカムを総体エビデンスとして評価するGRADEシステムという手法を開発しました．

カイ2乗検定（χ²検定）　chi-square test

観測されたデータの分布が，理論上の分布と比べて偏りがないかを検定するものです．カイ2乗検定は，カイ2乗適合度検定とカイ2乗分割表の検定（またはカイ2乗独立性の検定ともいいます）に分けられます．
たとえば，疾患分類を調査して，脳出血が38人，脳梗塞が11人，くも膜下出血が11人いたとします．このとき，いずれかの人数が他よりも多いとか，少ないとかの偏りがあるか調べます．これをカイ2乗適合度検定といいます．
また，過去1年の入院歴が｛あり，なし｝の分類と，過去1年の転倒歴｛あり，なし｝の関係で，人数を調査し，入院歴と転倒歴の関係を調べるとします．入院,転倒それぞれ｛あり，なし｝で区切られた2×2の分割表を作成し,入院歴ありで，かつ転倒歴がある者と，入院歴なしで，かつ転倒歴のない者が多いなどの関係を知りたいときにカイ2乗分割表の検定が適用されます．

片側検定　one-tailed test

　統計的仮説検定では帰無仮説を設定しますが，対立仮説の状態によって両側検定，片側検定と呼び分けます．
　例を挙げて説明しましょう．例えば，A群とB群の平均の差の検定を行うとします．このとき帰無仮説は“平均Aと平均Bには差がない”と仮定します．統計的仮説検定を行って確率が小さいとき（p<0.05）は，この帰無仮説が否定されますので，“差がある（対立仮説）”と判断します．
　しかし“差がある”という内容には，“平均Aが大きく平均Bが小さいという差”と，“平均Bが大きく平均Aが小さいという差”の2種類が存在します．これら2つの場合を考える差が両側検定となります．しかし“平均Aが大きく平均Bが小さいという差”しか考えない，ときには片側検定を行うことになるのです．
　相関係数の検定でも同様です．“握力と体重に相関がない”と仮定して検定したときに，p<0.05で否定されたとすると，“握力が強くなるほど体重は重い”という相関関係と“握力が強くなるほど体重は軽い”という相関関係の2つがありますが，これらのうち一方しか相関関係が成り立たないと考えて統計的仮説検定を行うのであれば，片側検定となります．ちなみに，差の検定で有意水準5％とするときは“平均Aが大きく平均Bが小さいという差”の1つを，p<0.05として検定するので，両側検定よりも差が出やすい状態になります．
　差があるというときは，平均Aが大きく平均Bが小さいという差か，平均Bが大きく平均Aが小さいという差か，どちらかを確かめたら良い（片側検定）はずです．しかし現状では，原則として両側検定を使用する，という考え方が一般的です．

カットオフ値　cutoff value

ある検査や測定結果の陽性・陰性を識別する数値のことであり，検査や測定の感度と特異度の関係を表したROC曲線を作成することで求めることができます．日本語では分割点，あるいは病態識別値などと呼ばれています．カットオフ値は，病態を識別するための検査・測定に用いられ，基準範囲を基本として正常とみなす範囲を決めるとき，その範囲を区切る値のことを意味します．すなわち，特定の疾患に罹患した，または罹患するリスクがあるということを分ける値です．
たとえば，ある虚弱高齢者の転倒リスクが高いか低いかを評価する場合，転倒リスクが高いとされるカットオフ値が示されているバランステストを用いて評価を行い,測定値とカットオフ値を比較することがあげられます．

カッパ係数（κ係数）　Kappa coefficient

データの型が名義尺度や順序尺度[→データの尺度を参照]で測られる評価の，信頼性（一致度）を評価するために使用される指標です．たとえば，検査者Aと検査者Bで変形性膝関節症患者の膝伸展筋力を測るときに，2人の検者の判定がどれくらい一致するかを数値（0～1の範囲）で表し，値が高いほど一致度が高いと判断します．

観察研究　observational study

人為的，能動的な介入（治療行為等）を伴わず，ただその場に起きていることや起きたこと，あるいはこれから起きることをみるという研究方法です． 観察研究は，その場で起きていることを断面的に調査すれば横断研究，過去にさかのぼって起きたことを調査すれば症例対照研究，これから起きることを調査すればコホート研究と分類されます．

感度　sensitivity

ある疾患を持つ人のうち，検査で陽性と正しく判定される割合です．たとえば，長谷川式簡易知能評価スケール（HDS-R）が20点未満のときに認知症であるという基準を仮定したとき，対象者100人中80人が20点未満でかつ，確定診断として真に認知症であったとき，HDS-Rの感度は80％となります．感度が高いということは，「陽性の者を陽性と正しく判定する可能性が高い」ということになります．

棄却検定　rejection test

　データを取ったとき，まれに通常では考えられないような大きな値や小さな値（外れ値）が得られることもあります．この場合，1つの外れ値と思われるデータが他のデータと同一の母集団と考えて良いかどうかを検定する手法が棄却検定です．棄却検定によって有意確率が有意水準未満（たとえばp<0.05）だったときに，帰無仮説「全て同一の正規分布から得られたデータである」は棄てられ，外れ値として認めることになります．
　棄却検定でよく使う手法としては，Smirnoff-Grubbsの検定，Thompsonの検定，増山による検定といった方法があります．
　これらの棄却検定は「データは正規分布する」という前提条件を満たさなければなりません．また，1つの外れ値に対して行う検定ですので，外れ値と思われるデータの回数分だけ検定を繰り返すことになります．さらに，棄却検定で棄却されたとしても，あくまで検定上なので，真に外れ値として認めてよいかどうかは，明らかに容認できる理論的裏付けが必要となります．従って現在の医学系研究においては，用いるべきではないという意見が有力となってきています．

記述的研究　descriptive study

　単に現状のデータの記述のみに止まる研究のことで，非実験的研究（non-experimental study）や非比較研究（non-comparative study）とも呼ばれます．
　比較対照群は置かないので，対象の割り付け（群分け比較）を行っておらず，症例報告や症例集積研究（ケースシリーズ研究）などがこれに相当します．たとえば，「退院後１年経過した脳卒中患者を追跡調査して，何％が“寝たきり状態”であるかを調べる」といった調査報告などがあげられます．

基準関連妥当性　crierion–related validity

　ある評価法とすでに確立されている評価法（黄金律（ゴールドスタンダード））との相関を求めることで判断します．基準関連妥当性は，それぞれの評価法の測定時期によって併存的妥当性と予測的妥当性に分けられます．併存的妥当性は，同時点で測定するもので，たとえば，新しく開発した評価法と既存の評価法との関連性があるかどうかを調べる研究があげられます．一方，予測的妥当性は，黄金律（ゴールドスタンダード）の評価法の測定がある評価法の測定より後に行い，ある評価法が測定後の将来の事象を適切に予測できるかどうかを表します．
 

基礎研究　basic study

研究室にて培養細胞や実験動物，または臨床材料（患者の献体など）を用いて基礎医学的な手法（生化学，生理学など）を行う研究と，ある疾患や動作を想定しながら健常者を対象として行う研究があります．基礎研究を積み重ねながら臨床研究に応用することによって，新しい評価法や治療法の発見につながっていきます．ヒトを対象とした基礎研究としては，健常者を対象として段差昇降動作時の筋活動や運動学的なデータを測定することなどがあげられます．

帰無仮説　null hypothesis

帰無仮説（H₀）とは，“差がない（差は0）”，“関係がない（相関が0）”などの無（＝0）を意味する仮説です．研究では通常，「運動療法前と比較して一定期間の運動療法後は，筋力が増強する」とか，「患者群の歩行速度は健常群の歩行速度よりも遅い」などの差（違い）を証明します．そのために統計的検定では“運動療法前後でも差がない”とか“患者群と健常群の歩行速度は差がない”などの帰無仮説を想定し，この仮説が成立する有意確率p値を求めます．有意確率が有意水準よりも小さければ（p<0.05のとき），対立仮説（H₁）を採択する（差がある）という判断をします．

級内相関係数（ICC）　intraclass correlation coefficients

ある検査の検者内または検者間信頼性（再現性というときもあります）の指標として用いられます．
ICCにはCase1，Case2，Case3の3種類があります．Case1は検者内信頼性を表す，ICC（1，1）やICC（1，k）というものです．Case2は検者間信頼性を表す，ICC（2，1）やICC（2，k）というものです．Case3は検者間信頼性を表す，ICC（3，1）やICC（3，k）というものです．Case2とCase3の違いは，Case2は絶対一致を調べるもので，Case3は相対一致を調べるものです．
ICC（1，1），ICC（2，1），ICC（3，1）は，検者内・検者間信頼性が，どれくらいあるのかを知るために使用します．ICC（1，k），ICC（2，k），ICC（3，k）は，複数回測定した平均値を使用したときの検者内・検者間信頼性を求めるときに使用します．別な例として，検者A，B，Cの3名で，患者5名の歩行速度を測定したとします．検者3人の一貫性（検者間信頼性）はどれくらいかを，ICC（2，1）で求めます．
検者B，Cよりも，検者Aの測定基準が異なるために，ほぼ0.5秒遅めに記録してしまうことがわかっているとき，もしくは，検者Aが0.5秒遅く測ってしまうストップウォッチを使用したなどのとき，検者A，B，Cが絶対一致することはなく，検者Aから0.5秒引いたときに一致すれば良いと仮定したときは，検者間信頼性としてICC（3，1）を使用します．つまり，ICC（2，1）は，検者A＝検者B=検者Cを仮定しており，ICC（3，1）は検者A+0.5秒＝検者B=検者Cとか，検者A＝検者B+10秒=検者Cとか，検者A+0.5秒＝検者B=検者C－1秒を仮定していることになります．
検者1名によって患者5名の歩行速度を3回ずつ測定して，3回測定の平均を用いて検者内信頼性を求めるときはICC（1，k）を求めます．この場合は，ICC（1，3）と表記します．ICC（2，k）もICC（3，k）も同様です．ICC（1，k）を最初に求めることはせず，まずはICC（1，1）を求めてから，何回測定した平均を用いたら良いかと考えてICC（1，k）を求めます．
全てのICCは，0～1の範囲をとり，一般に0.7程度以上のとき，高い信頼性があると判定します．

共分散分析　analysis of covariance（ANCOVA）

　平均の差の検定を行いたいときに，そのデータに影響を与える他のデータ（共変量）が存在する場合，共変量の影響を取り除いて差を検定する手法です．
　たとえば，電気療法の経時的効果を比較するために，腰痛患者に対して電気療法を行い，治療前，治療後1ヵ月，治療後2ヵ月，…，と疼痛の程度を評価します．治療前から治療後にかけて疼痛の程度が変化するか（差があるか）どうかを知りたいとき，年齢が低い例や治療前の罹病期間が短い例において効果が得られやすい可能性があります．そこで年齢や罹病期間を共変量として，それらの影響を取り除いた治療による疼痛の差を検定することができます．

共変量　covariate

分散分析を行うときに解析に含めるデータのうち，連続量で量的に表される変数のことをいいます．結果と“共”に変わる原因と思われる“変量”というわけです．回帰分析で呼ぶところの説明変数（独立変数）と同等です．これに対して，質的に表される変数は要因と呼ばれます．
たとえば，歩行速度に対するブルンストロームステージⅠ～Ⅵで分けた6群，性別で分けた2群，年齢の影響（差）を見るときに，ブルンストロームステージと性別は要因，年齢は共変量と呼びます．

局所管理　local control

　フィッシャーの三原則の一つ．データを記録するとき，例えば実験を行う時間帯や場所（系統誤差）に影響を受ける可能性があります．その際に実験を行う時間帯や場所を均等にした条件（実験計画法の用語で，ブロックといいます）を作り，そのブロック内でのバックグラウンドができるだけ均一になるように配慮することが「局所管理」です．「局所管理」によって，「無作為化」よりも，さらに系統誤差を小さくすることができます．
　例えば，比較したい条件がA，B，Cの3つあり，1日に6回の実験ができる場合を想定します．午前の測定ではやや高めに，午後の測定ではやや低めに記録される（系統誤差）ことがわかっているとします．そこで，各条件に午前と午後の測定における偏りが無くなるように調整する方法が「局所管理」です．「局所管理」は次に示すように実験を行う時間を午前と午後の2つのブロックに分けてブロック内にA，B，Cの条件が均等に入るようにします．高めに測定される午前と，低めに記録される午後のバックグラウンドがA，B，C，それぞれの条件に均等に割り振られて，互いにその効果を相殺することができるメリットがあります．
 

	1日目	2日目	3日目
処理（午前）	ABC	CAB	BCA
処理（午後）	BCA	ACB	CBA

なお，フィッシャーの三原則をすべて満たすこの例では，乱塊法による実験デザインと呼ばれることもあります．

Kruskal-Wallisの検定 　Kruskal-Wallis test

1元配置分散分析に相当するノンパラメトリックな手法（ノンパラメトリック検定）です．1元配置分散分析とは，3群以上の平均を比較し，差があるかないかを検定するパラメトリックな手法（パラメトリック検定）です．これに対して，正規分布に従わない3群以上の中央値を比較するために，1元配置分散分析の代わりとして用いられる検定です．
たとえば，運動をしていない群，軽い運動群，強い運動群の3群に対して，握力に差があるかという検定を行いたいとき，何れかの群の握力が正規分布に従わない場合は，Kruskal-Wallisの検定を適用します．それによって，これらの群間の中央値に差があるかどうかを判断できます．

クラスター分析 cluster analysis

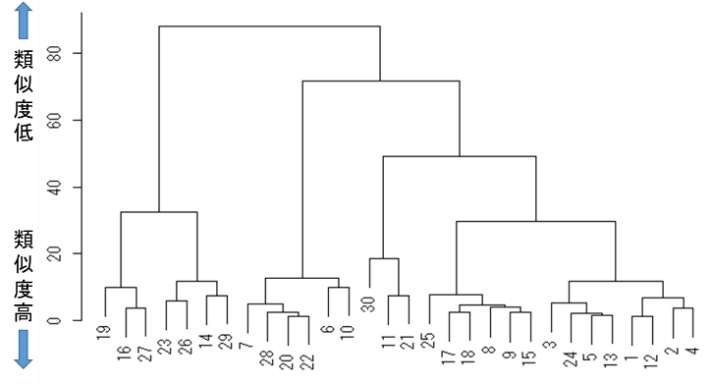
　複数の変数を，ある属性のもとで類似しているいくつかの群（クラスター）に分類する探索的な手法で，似たもの同士を集める分析です．変数は量的データでも質的データでも適用可能です．クラスター分析はさらに，類似度の大きさで順次分類する手法で，階層構造を図式化したデンドログラムで表される階層的手法と，予めクラスターの数を決めて分類する非階層的方法に大別されます．
　下図は被験者30名の身体測定（身長，体重，体脂肪量）のデータのデンドログラムです．縦軸は類似度を表し，横に各被験者の位置を表しています．これはクラスター同士が，どの段階でまとめられたかを示すもので，クラスターの階層的構造を把握するのに有効です．

クリニカルクエスチョン　clinical question

クリニカルクエスチョンは，臨床的疑問のことであり，病態・評価・治療・リスク・予防に関するものなど様々な種類があります．EBPTの実践において適切な治療方針や根拠を導き出すためには，最初のステップとして，このクリニカルクエスチョンを，「①どのような患者に（Patient），②どのような評価・治療をしたら(Intervention)，③何と比較して(Comparison)，④どのような結果になるか(Outcome)？」という４つの要素に定式化し，文献検索を行いやすいように整理します．この定式化の手法は，４つの要素の頭文字をとってPICO，あるいはIをE（Exposure：暴露）に変えてPECOと呼ばれています．
たとえば，2か月前よりテニスのバックハンドストローク時に右肘外側部に疼痛がある患者に対して，疼痛の軽減目的に超音波療法とマッサージのどちらが効果的かについて考えている場合には，P:慢性的なテニス肘の患者に対して，I:超音波療法を実施した場合と，C:マッサージを実施した場合で，O:疼痛軽減効果に違いがあるか？というふうに定式化します．

クロスオーバー試験　crossover trials

　対象を2群に分け，各群に別々の治療を行い評価した後に，各群の治療法を交換して再度評価する方法です．交差試験とも呼ばれています．この試験のメリットとしては，必要な症例数が少なくなることがありますが，デメリットとしては，試験期間が長くなること，症状が変化しやすい急性期や回復期の方は，前の治療条件の影響が次の治療条件の結果に影響を与える可能性があるなどがあげられます．

クロンバックのα係数 Cronbach’s coefficient alpha

　複数の検者によって検査・測定されたデータの信頼性（精度，再現性）を意味します．つまり，複数の検者が検査・測定を行ったときに値がどれくらい一致するか，検者どうしの一貫性およびバラツキを表す指標になります．
　たとえば，検者A，B，Cの3人が患者6人を対象として，膝伸展筋力を1回ずつ測定したときの検者3人の一貫性が検者間信頼性です．また，検者A，B，Cの3人が患者6人を対象として，膝伸展筋力を5回ずつ測定し，その5回測定の平均を用いて検者3人の一貫性を求める場合も検者間信頼性となります．
　検者間信頼性を求める手法として，データの型[→データの尺度を参照]が比率尺度や間隔尺度で測られた場合には級内相関係数（ICC）のCase2（たとえばICC（2，1）など）およびCase3（ICC（3，1）など）が用いられ，名義尺度や順序尺度で測られた場合にはカッパ係数（κ係数）が用いられます．

回帰分析　regression analysis

　1つの変数（説明変数（独立変数））から1つの連続データ（目的変数（従属変数））を予測するとき，もしくは説明変数（独立変数）が目的変数（従属変数）に及ぼす影響度を知りたいときに用いられます．この方法は単回帰分析，直線回帰，最小2乗回帰ともよばれます．たとえば，健常者を対象に目的変数（従属変数）をADL尺度の得点，説明変数（独立変数）を歩行速度として回帰分析を行うと，ADL尺度の得点に対する歩行速度の影響度を知ることができます．

CARE声明　case reports statement

　症例報告の質を改善することを目的として，報告すべき項目がチェックリストとして作成されたもので，caseのcaと reportsのreを合わせて，CAREと名付けられています．チェックリストは，タイトル，症例情報，臨床的意義，経過，評価，介入方法，フォローアップ，考察，介入に対する症例の主観，説明と同意など30項目で構成されています．このチェックリストを活用することで，症例報告の構成を理解することができ，必要な情報が漏れなく正確に記載されることでより透明性の高い論文が増えることが期待されています．ホームページ（http://www.care-statement.org/index.html）にアクセスすると，チェックリストとテンプレートが英文でダウンロードできるようになっています．
 

傾向スコア　propensity score

　1983年にRosenbaumとRubinによって考案され，近年，大規模な観察研究で使われるようになった統計解析の手法です．まだ確立した方法はないため，様々な手順が考案されています．
　理論は非常に難しいのですが簡単にいえば，複数の交絡因子を調整する手法です．一つの例を挙げましょう．1年後のADL（FIMの得点）というアウトカムに対して，｛しゃがみ込みができる・できない｝という影響因子を仮定したとします．しかし，しゃがみ込みのできない者に，高齢者，男性，下肢筋力の弱い人が多い場合，しゃがみ込みのできる人との背景因子が異なりますので，ADLは単純比較できません．
　そこで，しゃがみ込みができる・できないを目的変数（従属変数），年齢，性別，下肢筋力を説明変数（独立変数）として多重ロジスティック回帰分析を行い，予測確率（0～1の範囲をとる数値）を算出します．この予測確率は年齢，性別，下肢筋力という交絡因子群を一本化した，いわば交絡因子の総合得点に相当します．これが傾向スコアとなります．
　次に，しゃがみ込みができる人と，できない人で傾向スコアを比べて，似通った人たちでグループを作ります．例えば0～0.2のしゃがみ込みができる人とできない人，0.2～0.4のしゃがみ込みができる人とできない人，…，0.8～1のしゃがみ込みができる人とできない人というようにマッチングします．傾向スコアが0.2未満の人は，しゃがみ込みができる人だけとか，傾向スコアが0.8以上の人は，しゃがみ込みのできない人だけというときは，傾向スコアの範囲が0.2～0.8となる人だけの対象でマッチングします．その後に，改めて｛しゃがみ込みができる・できない｝という群分けで，FIMに差があるかどうかを検定します．マッチングをしますので，かなり多くの対象者数が必要となります．
　これは傾向スコアによるマッチング法ですが，層別解析する方法や，傾向スコアそのものを多変量解析の説明変数（独立変数）として解析に含める方法もあります．

決定係数（R²）　coefficient of determination

　重相関係数Ｒを2乗した値です．重回帰分析における実測値のバラツキ（分散）に対する予測値のバラツキ（分散）の割合で，重回帰式の適合性を評価する指標となります．絶対的な基準ではありませんが，Ｒ²≧0.5であれば適合度が高い，つまり重回帰式の予測制度が高いといえます．複数の重回帰分析の結果を比較して，適合度の優劣を決めたいときに，決定係数の大きい方を選ぶことがあります．ただし，比較する重回帰分析の結果は，説明変数（独立変数）の数が等しい時に限ります．
　自由度調整済み決定係数も複数の重回帰分析の結果を比較するときに使用する決定係数ですが，こちらは説明変数（独立変数）の数が等しくなくても比較可能となります．決定係数は説明変数（独立変数）の数が多くなると自動的に大きくなるという欠点を補うため，説明変数（独立変数）の数で調整した決定係数を自由度調整済み決定係数と呼びます．

研究計画法　research proposal

エビデンスが不十分で臨床判断が難しい場合や，日々遭遇するクリニカルクエスチョンに関して網羅的に文献検索を行ったうえで解決できない問題に対しては，自ら臨床研究を行い，エビデンスを構築していく必要があります．臨床研究では，やみくもにデータをとっていくのではなく，研究を開始する前にあらかじめ，臨床でのクリニカルクエスチョンを明確にし，研究のテーマとなる具体的なリサーチクエスチョンと研究仮説を立てて，その仮説を確実に検証するために研究計画書を作成することが大切です．研究計画書には，仮説を検証することでの臨床的意義や，研究デザイン，対象者の採用基準や除外基準，仮説を客観的に検証するための手順や必要な機器，統計解析の方法も含めて記載しておきます．予備実験を実施して研究計画書を修正し，倫理審査を受けたうえで本実験に入ります．原則として本実験開始後は，研究計画を変更することはできませんので，適切な文献レビューと丁寧な予備実験を通して入念な研究計画を立てる必要があります．

研究デザイン　study design

研究を計画するにあたり，対象や介入方法，評価･測定方法，評価期間などを決めるための，様々な研究の種類です．症例研究や症例報告などの記述的研究と，観察研究（横断研究，症例対照研究，コホート研究など）や実験的研究（ランダム化比較試験（RCT）など）といった分析的研究に分けられます．

検者間信頼性　inter-rater reliability

　複数の検者によって検査・測定されたデータの信頼性（精度，再現性）を意味します．つまり，複数の検者が検査・測定を行ったときに値がどれくらい一致するか，検者どうしの一貫性およびバラツキを表す指標になります．
　たとえば，検者A，B，Cの3人が患者6人を対象として，膝伸展筋力を1回ずつ測定したときの検者3人の一貫性が検者間信頼性です．また，検者A，B，Cの3人が患者6人を対象として，膝伸展筋力を5回ずつ測定し，その5回測定の平均を用いて検者3人の一貫性を求める場合も検者間信頼性となります．
　検者間信頼性を求める手法として，データの型[→データの尺度を参照]が比率尺度や間隔尺度で測られた場合には級内相関係数（ICC）のCase2（たとえばICC（2，1）など）およびCase3（ICC（3，1）など）が用いられ，名義尺度や順序尺度で測られた場合にはカッパ係数（κ係数）が用いられます．

検者内信頼性　intra-rater reliability

　1人の検者が検査・測定を複数回繰り返したときの信頼性（精度，再現性）を意味します．つまり，検査・測定を繰り返したときに値がどれくらい一致するか，1人の検者自身による一貫性およびバラツキを表す指標になります．
　たとえば，1人の検者が10人の患者を対象として，片脚立位保持時間を1回ずつ測定したときの一貫性が検者内信頼性です．また，1人の検者が10人の患者を対象として，片脚立位保持時間を3回ずつ測定した平均を用いて一貫性を求める場合も検者内信頼性となります．
　検者内信頼性を求める手法として，データの型[→データの尺度を参照]が比率尺度や間隔尺度で測られた場合には級内相関係数（ICC）のCase1が用いられ，名義尺度や順序尺度で測られた場合にはカッパ係数（κ係数）が用いられます．

検定力　 power of test

真に「差がある」とか「相関がある」といった対立仮説が成立するときに，正しく「差がある」，「相関がある」という対立仮説を判定する確率（1－β）のことです．検出力ともいいます．通常は1－β＝0.8や1－β＝0.95に設定します．
脳卒中群と健常群の握力の差の検定をするとします．そのとき，脳卒中群と健常群の母集団どうしの平均に，本当に（真に）差があるとき，検定によって「差がある」と正しく判定する確率（1－β）が検定力です．

交互作用　interaction

原因変数と結果変数の因果関係に対して，強める（または弱める）作用を表す変数のことです．強める例をあげると，下肢筋力増強運動（原因変数）を一定期間行わせて，垂直跳び距離が高くなった（結果変数）という研究をしたとき，下肢筋力増強運動の期間が長い者は，短い者よりも高く跳べるでしょう．このとき「下肢筋力増強運動と運動の期間は交互作用がある」といいます．

効果量　effect size

　効果量は，データの単位に依存しない標準化された効果の程度を表す指標です．効果とは，データの差・影響・相関・連関のことです．効果量は単位の異なる研究から得られた効果の比較や人数の異なる研究から得られた効果の比較が可能です．例えば，論文Aの報告で若年群と高齢群の膝伸展筋力の差が平均30±10kgだったとします．次に論文Bの報告では若年群と高齢群の膝伸展筋力の差が平均20±30N（ニュートン）だったとします．この結果を見て，論文BよりもAの差が大きいとは言えません．それはデータの単位がkgとNで異なるからです．どちらの論文の結果の差が大きいかを比べたいときは，効果量を求めて比較すると明確になります．なお，効果量はノンパラメトリックな手法（ノンパラメトリック検定）が対象となるデータでも算出できるものがあります．
　また効果量には，いくつか種類があり，特にrという効果量と，dという効果量の2種類が代表的です．rもdも計算方法が異なるだけで意味は同一なのですが，rは0～1（もしくは0～-1）の範囲をとるので理解しやすいメリットがあります．従って，通常はrを利用します．
　効果量を計算できる統計ソフトは少ないですが，ウェブサイト(http://www.mizumot.com/stats/effectsize.xls)で無料配布されているファイルを使用するのが便利です．
　以下に，効果量の判定基準を記載します．
 

検定	指標	効果量の基準			補足
		小	中	大
t検定（差の検定としての）	r	0.1	0.3	0.5	対応のあるt検定，2標本の差の検定で同一値．rとdの2種類ある．通常はrを利用
	d	0.2	0.5	0.8
分散分析	η2	0.01	0.06	0.14	多重比較法はt検定（差の検定としての）を参照
相関	r	0.1	0.3	0.5	相関係数そのままである
カイ2乗検定（χ2検定） (2×2分割表)	φ	0.1	0.3	0.5	連関係数である
カイ2乗検定（χ2検定） (上記以外の分割表)	クラメールのV	0.1	0.3	0.5	連関係数である
ノンパラメトリックな手法（ノンパラメトリック検定）	r	0.1	0.3	0.5	Mann–WhitneyのU検定，Wilcoxonの符号順位検定，Kruskal-Wallisの検定，Friedmanの検定で求められる検定統計量Zを用いてr＝Z/√n
(重)回帰分析	R2	0.02	0.13	0.26	決定係数である

交絡因子　confounding

原因変数と結果変数の因果関係に対して，間接的に影響する変数のことです．交絡因子は『条件①：原因変数と関連』して，かつ『条件②：結果変数と因果関係を持つと考えられる』という2条件を満たさなければなりません．
下肢筋力（原因変数）と，垂直跳び距離（結果変数）の関係を見るという研究をするとき，若年者は筋量が多いゆえに高く飛ぶでしょうし，高齢者はその逆となります．このとき“年齢”は①下肢筋力と関連し，②垂直跳びと因果関係を持つと考えられるので交絡因子となります．交互作用と非常に似通っており，交絡因子＝交互作用となることもありますが，上述の条件2つを満たす場合のみ，交絡因子とみなします．

コクラン共同計画　the Cochrane collaboration

ヘルスケアの介入の利益とリスクに関するシステマティックレビューを，用意し，手入れをし，アクセス性を確実にすることにより，人々が十分に知らされた意思決定ができるようにすることを目的とする国際プロジェクトを意味します．英国の国民保健サービス（National Health Service :NHS）による根拠にもとづく医療政策と実践，またその定量的な評価の一環として始まり，治療法の評価方法は，ランダム化比較試験（RCT）を基本とすべきとされています．この計画は，様々な医療上の介入について，既存の臨床研究を幅広く集め，きちんとした手法に則ってまとめた上でわかりやすい形で提供することを目指しています．コクラン共同計画で実施されたシステマティックレビューは，コクランンライブラリというデータベースにまとめられインターネット上で公開されています．

誤差の許容範囲 limits of agreement（LOA）

　検討している測定方法を用いて複数回測定した際の測定値の変化量が，推定された誤差範囲以内のものならば，その変化は誤差によるものと判断されます．推定される誤差の範囲を誤差の許容範囲といいます．
　たとえば，最大歩行速度を2回測定し，誤差の許容範囲が-1.5秒から3秒と算出された場合，2回目の測定は1回目の測定よりも1.5秒速い値から3秒遅い値に収まると推定できます．[→MDC95を参照]

コックス比例ハザードモデル　Cox proportional hazard model

　コックス比例ハザード分析とかコックス比例ハザード回帰，コックス回帰，比例ハザード分析など，多様な呼び方をされることがあります．これは，生存分析の多変量解析となります．イメージとしては，ログ・ランク検定の多変量解析版と考えてもらえばよいでしょう．
　時間の経過で発生する｛生，死｝，｛転倒あり，転倒なし｝，｛歩行可能，歩行不可能｝などのイベントに対して，調査した複数の項目の何が影響するかを調べるための統計的手法です．数理的には，ロジスティック回帰分析と非常に似通っていますので，データの尺度や分布は問わない分析方法です．異なるのは，時間の経過で発生するという，時間的な要素を考慮している点です．
　例として，地域在住の高齢者50名を対象として，1年間で転倒が起こったか，起こらなかったかを調べたとします．同時に，調査開始から何ヶ月後に転倒が起こったか，起こらなかったかを調べます．ある者は5ヵ月目に転倒していたかもしれません．また，ある者は8ヵ月目には転倒していませんでしたが，それ以降は調査できなかったとします．この例で，5ヵ月，8ヵ月という期間は「観察打ち切りの期間」となります．その観察打ち切りの期間を考慮した転倒の有無に対して，膝伸展筋力や片足立ち時間などの，複数の，どういった項目の組み合わせで転倒発生を早めているかを調べるときに，コックス比例ハザードモデルを適用します．

コホート研究　cohort study

ある特定の疾患の起こる可能性がある要因・特性を考え，対象集団（コホート）を決め，その要因・特性を持った群（曝露群）と持たない群（非曝露群）に分け，疾患の罹患や改善・悪化の有無などを一定期間観察し，その要因・特性と疾患との関連性を明らかにする研究方法です．原則として，コホート研究は介入をせず，観察のみで行われる研究です．利点としては，ある特性に対する結果の観察に優れ，対象の割り付け時にバイアスを可能な限り避けられ，対象から直接データを集めることができることなどがあげられます．欠点としては，時間・費用的効率が悪く，開始時点の対象集団割り付け時に疾患に関与する背景因子に気づかない恐れがあることなどがあげられます．
たとえば，糖尿病患者における身体活動量と，血糖値や体重との関連を調査するために，身体活動量に応じて対象を割り付けし，身体活動量と血糖値・体重との関連を検討するといった研究デザインです．

Kolmogorov-Smirnovの検定　Kolmogorov-Smirnov test

データの母集団が正規分布しているかどうかを検定する手法の一つです．検定の結果，p<0.05で有意となったときは「正規分布していない」と判断し，p≧0.05のときに「正規分布していない，とはいえない（＝正規分布している）」とみなします．この検定の欠点は，サンプルサイズが少ないとき（およそn≦100）は，精度が悪いという点です（統計ソフトによっては補正していることがあります）．

コンソート声明　CONSORT Statement

コンソート声明（Consolidated Standards of Reporting Trial　Statement）は，国際的に定められた臨床試験報告に対する統合基準のことであり，ランダム化比較試験（RCT）の報告内容の改善，読者の臨床試験の実施の理解，試験結果の妥当性の評価を，可能とすることを目的に発表されています．1996年に初版コンソート声明が開発された後，改訂が繰り返されて現在の最新版はコンソート2010となっています．コンソート声明は，25項目のチェックリストとフローチャートで構成されています．コンソート2010を利用することで，ランダム化比較試験（RCT）の著者と査読者が出版のための原稿を同じように批判的吟味することが可能となり，明快かつ透明性の高い報告を支援する意義があると期待されています．

構成概念妥当性 　construct validity

　ある評価法が，測定しようとする概念や特性をどれだけ適切に反映しているかを意味します．言い換えると，全体的に見て個々の因子を組み合わせたとき，測定項目全体が意図するものを測っているかどうかに関する妥当性のことをいいます．たとえば，高齢者の転倒リスクの評価を行う場合，柔軟性，筋力，持久性，バランス，認知機能など関連性のある複数の因子を組み合わせることで，構成概念妥当性を高くすることができます．
 

コクランズの統計量Q値　Cochran's Q statistics

　メタ分析において個々の研究結果の違いやばらつきがないかを確認する異質性の検定の一つであるCochran Q testで求められた数値のことで，フォレストプロット内に示されます．コクランズの統計量Q値は，p値が5%より小さい場合に有意差あり異質性が高いと判断します．異質性の検定として用いられるI² 統計量 は，研究の数や指標に左右されにくいのに対して，コクランズの統計量Q値は，研究の数に影響を受けやすいといわれています．
 

クオリティオブエビデンス　quality of evidence

　Summary of findings （SoF）表の項目の1つで，研究で得られた効果推定値(estimate of effect)の正しい確信がどの程度であるかを示すものです．High（今後の研究によっても，効果推定値に対する確信性が変わる可能性は非常に低い）, Moderate（今後の研究が効果推定値に対する確信性に対して重大なインパクトを持つ可能性があり，推定値は変わりうる）, Low（今後の研究が効果推定値に対する確信性に対して重大なインパクトを持つ可能性が高く，推定値は変わりうる）, Very low（推定値について非常に確信が持てない）の4段階にグレーディングされ，アウトカムごとに集められたエビデンスの質をHighから順にスタートして評価していきます．問題が見つかるごとにグレードを下げ，最終的に4段階のいずれかにグレーディングされます．重要な点は，複数のランダム化比較試験（RCT）から成るシステマティックレビューであっても必ずしもHigh判定であるとは限らないことです．
 

GRADEシステム　GRADE system

　Grading of Recommendations Assessment, Development and Evaluationの略です．
　GRADEシステムは，システマティックレビューや診療ガイドラインにおけるエビデンスの確実性を評価し，推奨の強さを決定するための透明性の高いアプローチとして開発されました．GRADEシステムは，ＰＩＣＯ（Patient/Population, Intervention, Comparison, Outcome）で定式化したクリニカルクエスチョン（clinical question, CQ）に対して，複数の研究を入手し，結果をアウトカムごとに統合した後に，各アウトカムの重要性をタスクフォース内の合意のもとに，患者にとって重大（7～9点），重要（4～6点），重要でない（1～3点）の9段階に分類し，患者にとって重大あるいは重要なアウトカムが推奨決定のための対象として用いられます．次にグレードを下げる5要因とグレードを上げる3要因の合計8要因に基づいて各アウトカムのエビデンスの質を評価し，全体としてのエビデンスの質が「高」，「中」，「低」，「非常に低」の4段階に判定されます．その後，ガイドラインパネルによって，ガイドラインとしての推奨の強さ（強い，弱い／条件付き）と推奨の方向（推奨する，推奨しない）がグレーディングされます．
 

コクラン・ハンドブック　Cochrane handbook

　コクラン・レビューを作成する著者のための手引きのことです．システマティックレビューの手法が更新されたり，利用者からの意見をもらったりしたことを反映するために，定期的に更新されています．インターネット（https://training.cochrane.org/handbook）にて無料で閲覧可能です．

固定効果モデル（メタ分析）　fixed effect model

　メタ分析において，複数の原著論文の結果からオッズ比・リスク比などの効果量を統合するときに，原著論文間の効果量＝効果+誤差と考えられるときに，固定効果モデルを使用します．Mantel-Haenszel検定（法）や　Peto法が，この固定効果モデルを仮定しています．
　かなりかみ砕いた簡単な例で説明すれば，複数の研究者が，ほぼ同質の対象に対して，同じ方法で，同じ評価基準を用いた研究を，ほぼ同じ環境で行ったときに，それぞれの研究者が得られる効果は同じ程度になるはずです．その効果を単純に統合する方法が固定効果モデルです．

感度分析　sensitivity analyses

　研究結果の因果関係を明確にするためには，交絡因子の完全把握が必要です．しかし，現実には不可能なので未測定の交絡因子が存在します．感度分析とは，未測定の交絡因子を統計解析に組み入れ， その影響力を推測したときの因果効果を確認する方法です．
　観察研究では，因果関係に関係する交絡因子をすべて把握することはできず，把握していたとしても測定できないこともあります．たとえば，転倒と下肢筋力低下の関係を検討する際に，交絡因子として立位バランスや認知の障害は評価していたけれど，めまいの有無や関節炎などは把握していなかったとします．この未測定の交絡因子が存在すると仮定して，結果にどの程度影響するかを推測し，結果や結論の頑健性を評価する重要な方法です．
 

改ざん（改竄）　falsification

　改ざんとは，研究方法・材料，研究過程，研究結果，文献等を意図的に有利な内容に書き換えて論文投稿，または口頭で発表する行為です．たとえば複数回測定したデータのうちから，研究者の意図する結果となるようなデータのみを抜粋したり，都合の悪いデータを削除して統計的検定の結果を有意にして発表することは改ざんとなります．

採用基準　inclusion criteria

　ある母集団から研究参加者を対象へと組み入れる過程においては，参加者の個々の特性や，研究参加に対する意思に基づき，その研究の対象として適しているかを判断する基準が必要であり，これを採用基準または組み入れ基準といいます．理学療法の臨床研究において採用基準となる個々の特性の具体例としては，年齢，性別，体格，地域，罹患疾患，身体機能，動作能力，運動習慣の有無などが挙げられます．

サブグループ分析　subgroup analysis

変形性股関節症患者を対象として，下肢筋力増強運動の効果を検証したいとします．対象の年齢層が広い範囲で構成されているとすれば，いくつかの年代別に分けた集団（サブグループ）ごとに解析を行って，どの年代でも効果が認められるかどうか確認する場合があります．このように，解析の対象となる集団全体ではなく，年代別や性別，疾患の重症度別などといったサブグループに分けて解析することをサブグループ分析といいます．

サンプリング　sampling

　研究において，選択基準を満たす集団（母集団）の調査は不可能に近いため，その中から標本（sample）を抽出しなければいけません．医学領域でよく使われる抽出方法（sampling）として，無作為抽出法（random sampling）があり，その手順によって，単純無作為抽出法，多段抽出法，層化抽出法などがあります．単純無作為抽出法，多段抽出法は母集団に番号をつけ，乱数などを用いて無作為に抽出する方法で，層化抽出法は，結果に間接的に影響する可能性がある要因ごとに群分けして抽出する方法です．しかし，無作為抽出法は大規模な調査であれば実施可能かもしれませんが，実際の臨床現場においては，自施設の入院患者30名など抽出条件を定めて選択することが多く，実施するには難しい方法です．無作為抽出法に従わない抽出法は，有意選出法（purposive selection）と呼ばれ，想定している母集団に近い小集団を想定して抽出する典型法などがあります．

サンプルサイズ　sample size

対象の数のことで，標本の大きさとも呼びます．研究報告では，一般的に「n」と略します．n≒∞の大きな集団（母集団）を全て調べるのは難しいので，対象者（標本）を数名選んで研究対象とします．
統計的検定を行うとき，サンプルサイズが小さいときは検定力が小さくなるゆえに，第Ⅱ種の過誤（βエラー）も大きくなります．サンプルサイズが大きいときは，検定力が大きくなり，第Ⅱ種の過誤（βエラー）は小さくなります．なお，第Ⅰ種の過誤（αエラー）はサンプルサイズによらず常に一定です．

Scheffeの多重比較法 Scheffe’s multiple comparison procedure

多重比較法のうちの1つの手法です．特徴は，分散分析と同じF統計量を用いるために，分散分析の結果と一致することです．また，単に群間比較だけではなく複数群をまとめたグループ間の差も検定できる点があります．健常群と膝関節疾患群，股関節疾患群におけるTimed Up and Go Testの差を検定するとき，3群の差を検定する方法や，健常群と，膝関節+股関節疾患群の2群にして差を比較することもできます．欠点としては，他の多重比較法よりも，有意差が出にくくなるという点です．

システマティックレビュー　systematic review

ランダム化比較試験（RCT）などの質の高い複数の臨床研究を，複数の専門家や研究者が作成者となって，一定の基準と一定の方法に基づいてとりまとめた総説のことをいいます．具体的には，明確で焦点が絞られた疑問から出発して，網羅的な情報収集を行い，集められた情報を批判的に吟味[→批判的吟味を参照]し，それらの情報を要約するという手続きがとられます．システマティックレビューには，同時にメタ分析を行っているものもありますが，その違いを理解しておくことが重要です．メタ分析との違いは，メタ分析の作成方法が必ずしもエビデンスに基づいていないのに対し，システマティックレビューはエビデンスに基づくことが必須であるという点です．また，メタ分析では，結果のまとめ方が定量的であることが必須であることに対し，システマティックレビューでは批判的吟味という過程を重視しており，定量的に結果を表すかどうかは問われません．ランダム化比較試験（RCT）を統合再分析しているコクラン共同計画の論文は，すべてシステマティックレビューと呼ばれています．

実験的研究　experimental study

　分析的研究のうちの介入研究を指し，実際に治療などの人為的な介入を行って，その効果や変化をみる研究です．ランダム化比較試験（RCT）や準ランダム化比較試験，クロスオーバー試験，前後比較試験，対照群をもたない研究など，何らかの介入を実施した研究のことを指します．たとえば ，「退院時に歩行が自立していた脳卒中患者を，退院後もリハビリテーションを継続した群とリハビリテーションを行っていない群に分け，１年後に再調査し，寝たきり率に差があるかどうかということを解析する研究」などがあげられます．

質的データ qualitative data

データの尺度のうち，名義尺度と順序尺度が質的データに含まれます．名義尺度のように順序をつけることができないデータや，順序尺度のようにデータの間隔が一定でないデータです．統計解析では，質的データに対してノンパラメトリックな手法（ノンパラメトリック検定）が適用されます．

四分位数　quartile

データを小さい順から並べたときに，25％値，50％値，75％値で区切ると4区分に分けられます．これを四分位数といいます．小さい方から第1四分位数（25％値），第2四分位数（50％値＝中央値），第3四分位数（75％値）と呼びます．
たとえば，0から1刻みに100までのn=101のデータがあったとします．このとき，0％値は「0」，25％値は「25」，50％値は「50」，75％値は「75」，100％値は「100」となります．通常は，正規分布に従わないデータに適用されます．四分位数を表すグラフとしては箱ひげ図があります．

Shapiro-Wilkの検定　Shapiro-Wilk test

データが正規分布しているかどうかを検定する手法です．検定の結果，p<0.05で有意となったときは“正規分布しない”と判断し，p≧0.05となったときは“正規分布していない，とはいえない（＝正規分布している）”とみなします．

重回帰分析　multiple regression analysis

1つの連続データ（目的変数（従属変数））に対して，2つ以上の変数（説明変数（独立変数））がどのように影響するかを知りたいときに用いる，多変量解析の1つです．たとえば，健常者を対象に，目的変数（従属変数）を10m最大歩行速度，説明変数（独立変数）を膝伸展筋力，片脚立位保持時間，全身反応時間として重回帰分析を行うと，10m最大歩行速度に対して，3つの説明変数（独立変数）がどのように影響するかを知ることができます．

重相関係数　multiple correlation coefficient

重回帰分析を適用したときに得られる目的変数（従属変数）の予測値と実測値との相関係数で，回帰式の予測精度の指標の一つとなります．重相関係数は大文字のRで表記されます．0≦R≦1の範囲をとり，1に近づくほど予測の当てはまりがよいことを意味します．なお，Rを二乗した決定係数も，同様に回帰式の予測精度の指標として用いられます．

縦断研究　longitudinal study

　研究を時間要因によって分類したときの一つで，横断研究のように現時点での暴露の有無・程度を調べるのではなく，過去にさかのぼって，または将来にわたって，ある特定の対象に対して暴露の有無などを調査し，ある程度の期間を経たデータをとる研究です．　
　後ろ向き研究（症例対照研究）と前向き研究（コホート研究・ランダム化比較試験（RCT））が相当します．
 

主効果 main effect

　分散分析において，検定した要因で有意に差が認められるときは，主効果（または単純主効果）ありと呼ぶことがあります．分散分析では，主効果，交互作用が判断の基準になります．
　いま，健常者10名を対象として，階段を昇る時の膝伸展筋活動を記録したとします．階段の高さは①10cm，②15cm，③20cmに設定します．また，階段を昇るときの速さを①速い，②普通，③遅いの3段階にしたとします．このとき，階段の高さの要因，階段を上る速さの要因で差があるかどうかを知るために，2要因の分散分析（2元配置分散分析）を行うことになります．
　もし，高さの要因で有意な差が認められた場合は「階段の高さには主効果が認められた」といいます．また，速さの要因で有意な差が認められなかった場合は，「速さの要因では主効果は認められなかった」といいます．さらに階段の高さと速さの交互作用に有意差が認められたときは「階段の高さと速さの要因間で交互作用を認めた」といいます．

主成分分析　principal component analysis

　複数の変数を1つにまとめて，変数群のもつ構成概念（主成分）を探る手法です．重回帰分析やロジスティック回帰分析のような多変量解析で，多くの説明変数を対象とする場合に変数間の相互関係を把握することにも利用されます．
　相関係数を利用して，関連の強い似通った変数をまとめていきます（第1主成分）．関連の強さは主成分負荷量として求められます．次に，似通っていない変数群に対して，別の視点から再度まとめていきます（第2主成分）．このようなことを繰り返して，いくつかの主成分を作成します．
　例として，体力測定を行い，各評価項目（身長，体重，上肢長，下肢長，垂直跳び，走り幅跳び，立位体前屈）をまとめたい（構成概念を探りたい）ときに，主成分負荷量が大きい値を示す変数を順次まとめていきます（第1主成分，第2主成分…）．仮に，第1主成分で身長，下肢長，体重，第2主成分で垂直跳び，身長，走り幅跳び，下肢長，第3主成分で立位体前屈，身長，上肢長と主成分負荷量が大きければ，第1主成分は体格，第2主成分は跳躍力，第3主成分は柔軟性を表す主成分とイメージできます．主成分の意味づけ（構成概念の解釈）は解析者の主観に委ねられます．

出版バイアス　publication bias

　研究結果の方向や，統計的に有意か否かによって，研究が出版されるかどうかが決まる場合に発生するバイアスのことを指します．有意差のない結果になった場合は，論文として発表されない可能性が高くなりますが，有意差のある結果ばかりが発表されていると，偏った情報しか入ってこないことになります．多数の小規模研究に基づいたシステマティックレビューは，その研究のスポンサーが研究結果に対して既得権益を持っている営利企業である場合に，特に出版バイアスの影響を受けやすいと言われています．ただし，研究者が未出版の研究をレビューに組み込む場合は，報告書の完全版を入手し，同じ基準を用いて出版済みの研究と未出版の研究の妥当性を評価する必要がありますが，出版バイアスの可能性を調べる様々な方法を使用しても，完全に満足のいく結果にはならないのが現状です．

準実験的研究　quasi-experimental study

　ランダム化比較試験（RCT）や準ランダム化比較試験以外の，ランダム割付を考慮せず，介入群と対照群を比較している研究のことを指します．対照群（比較群）をもたない研究もこれに含まれます．
 

症例集積研究　case series study

ある疾患をもつ患者群，または同じ治療を受けた一連の患者群のみを対象とし，その疾患の特徴を測定・調査した研究報告のことであり，対照群との比較は行わない研究方法です．横断研究として，その疾患をもつ患者群の現状を調べるために用いられることが多いです．
たとえば，人工股関節全置換術後の患者における，痛みの程度・質に関する調査を行うことや，腰部脊柱管狭窄症患者の下肢筋力を測定することなどが考えられます．

症例対照研究　case control study

ある疾患をもつ患者群とそれと比較する対照群に分けて，疾患の特徴や疾患の起こる可能性がある要因にさらされているかどうか，また背景因子の違いなどを比較し，関連を確認するための研究方法です．現在の要因や過去にさかのぼった要因を用いるため，横断研究または後ろ向き研究として分類されます．利点として，時間的・経費的な効率が良く，割り付けの際に症例数の調整ができ，症例数の少ない患者を対象とする研究で有利であることなどがあげられます．欠点としては，選択バイアスや情報バイアスの影響[→バイアスを参照]が入りやすいことなどがあげられます．
たとえば，変形性膝関節症の患者群と，性別や年齢を患者群と同じにした健常者の群（対照群）に分けて，転倒歴や歩行速度を比較するなどが考えられます．

除外基準　exclusion criteria

　ある母集団から研究参加者を対象へと組み入れる過程において，その研究の対象として不適格となるような参加者の特性がある場合や，研究参加に対する参加の許諾が得られない場合など，参加者を対象者から除外する際の基準のことを除外基準といいます．理学療法の臨床研究において除外基準となる個々の特性の具体例としては，年齢，性別，体格，地域，罹患疾患，身体機能，動作能力，運動習慣の有無などが挙げられます．

信頼区間　confidence interval

データの平均（標本平均）から母集団の平均（母平均）がどれくらいか，といった範囲を推定する指標が信頼区間です．95％信頼区間とは，95％の確率で母平均がその範囲に含まれることを表しています．この他に99％信頼区間が用いられる場合もあります．たとえば，脳卒中片麻痺患者10名の健側握力を測定して，95％信頼区間が14.7kg～23.2kgであったとき，n=∞のときの脳卒中片麻痺患者の健側握力は95％の可能性で14.7kg～23.2kgの間に存在すると推定できます．

信頼性　reliability

信頼性には，正確度（確度）と精度があります．正確度とは，真に100kgの重さのものを測ったときに，その100kgとどれくらいの差があるかを問題とします．かたや精度は，測る人がどれくらい一致するかを表す指標です．検者のバラツキを表す指標なので，検者全員が105kgで測っても精度は高いといえます．ここでいう信頼性は，精度のことをいい,再現性ともいいます．
ある評価・測定を繰り返し何度行っても，ほぼ同じ結果が得られたとき，信頼性が高い評価・測定であるといわれます．信頼性を検討している先行研究では，Pearsonの相関係数, あるいは級内相関係数（ICC），クロンバックのα係数,カッパ係数（κ係数）などの係数を用いて信頼性の程度を表します．

診療ガイドライン　medical guideline

医療者と患者が適切な臨床判断ができるよう支援することを目的として，体系的な方法に則って作成された総説論文のことをいいます．具体的には，同じく総説論文であるシステマティックレビューとは異なり，ガイドラインでは，一つの限定された問題を取り上げるのではなく，現実的にとり得る医療の選択肢を網羅的に取り上げています．システマティックレビューは，エビデンス主導であり，エビデンス自体を提示するのに対し，ガイドラインではエビデンスの提示だけでなく，エビデンスをどのように臨床に適用するかについても言及します．また，ガイドラインの作成には関わる人の範囲が広いことも特徴です．検討対象となる疾患についての専門家だけでなく，臨床疫学者，生物統計学者，患者などが関与しています．作成の基本原則としては，「根拠に基づいた医療（evidence based medicine）」の手順に則って作成することが示されています．

スクリーニング　screening

　ある集団に対して評価を行うことで，身体に異常が起きている，または，異常が起こる可能性が高いことが疑われる状態であるどうかを識別することです．臨床では，評価にかかる時間や費用が少なく，感度，特異度，信頼性が高い評価を選択する必要があります．そして，スクリーニングを実施する際には，評価を受ける人に精神的，身体的，経済的な負担がかかること，結果が正常であっても実際は異常であったり，逆に異常であっても実際は正常であったりすることがあることを理解しておく必要があります．たとえば，入院初日に患者の転倒リスクが高いかどうかをスクリーニングする評価を行い，転倒リスクが高い場合には，安全対策を実行することがあげられます．

STARD声明　Standards for Reporting of Diagnostic accuracy

　この声明は，診断の研究報告のための指針です．診断研究報告の標準化を目的として策定されました．
　タイトル，イントロダクション，方法，結果，考察などの項目に対して25項目のチェックリストからなります．診断確度について評価したことがわかるような感度，特異度，尤度比といった内容について記載されているかなどを確認します．STARD2015からは，チェックリストが30項目になっています．医学雑誌編集者国際委員会（ICMJE）が，研究デザインに関する報告ガイドラインとして参考にすることを推奨する，EQUATOR Networkや米国国立医学図書館のResearch Reporting Guidelines and Initiativesでも紹介されています．http://www.stard-statement.org/にアクセスすると，チェックリストが英文でダウンロードできます．日本語に翻訳した内容は，名郷の文献²⁷⁾を参照してください（チェックリストは25項目）．

STROBE声明　the Strengthening the Reporting of Observational Studies in Epidemiology Statement

　観察研究の報告の質を改善することを目的として，報告すべき項目をチェックリストとして作成されたものです．多くの医学研究は観察研究であるにも関わらず，その研究の強みや弱み，および一般化可能性に関する記載が十分にされていることが少ないといわれています．この声明は，論文の「タイトル」から「考察」に至る各項目に関連した22項目のチェックリストで構成されており，研究報告時に含めるべき内容が記載されています．
　ホームページ（http://www.strobe-statement.org/index.php?id=strobe-translations）上では，日本語版のダウンロードも可能です．また，この声明が推奨する研究デザインの範囲は，コホート研究，症例対照研究，横断研究という主要なデザインと定められました．この声明は，観察研究の報告の質を向上させるための著者への支援となるだけでなく，雑誌の査読者，編集者，および読者が，論文の批判的吟味や解釈を行う上でも有用とされています．

Spearmanの順位相関係数　Spearman’s rank correlation coefficient

母集団が正規分布に従わないデータどうしの相関係数を求めるときは，Spearmanの順位相関係数が用いられます．ρ（ロー）またはrsと表記され，－1から1の範囲をとります．0から1の範囲にあるときは一方の変数が大きくなるに従い他方も大きくなるという正の相関が，－1から0の範囲にあるときは一方の変数が大きくなるに従い他方は小さくなるという負の相関があることを意味します．0のときは2変数が全く無関係で，1に近づくほど，または－1に近づくほど変数間の関係が強いことになります．

正規分布　normal distribution

データの分布で，平均が中心部分の頂上にある左右対称な「山型」あるいは「つり鐘型」の形状をしているものを正規分布といいます．分布の形状をみる際には, 縦軸に分布の頻度,横軸にデータ区間をとって図で表したヒストグラム[→度数分布を参照]を参考にします．
統計的解析では，データの母集団が正規分布しているとみなされる場合はパラメトリックな手法（パラメトリック検定）を適用し，正規分布していないとみなされる場合はノンパラメトリックな手法（ノンパラメトリック検定）を適用して，使い分けます．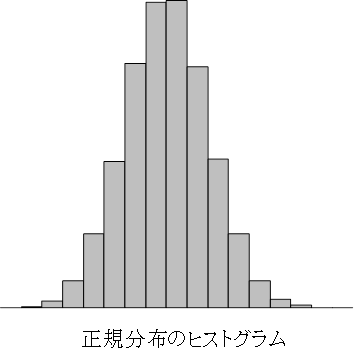

正準相関分析　canonical correlation analysis

　重回帰分析は1つの目的変数に対して，複数の説明変数が影響することを調べる手法です．これに対して，複数の目的変数に対して，複数の説明変数が影響することを調べる手法が正準相関分析です．
　たとえば，体力測定を行い，身長，体重，上肢長，下肢長の変数群（説明変数群）が，握力，背筋力，垂直跳びの変数群（目的変数群）にどのように関係するか知りたいときに，目的変数群と説明変数群の関連を正準相関係数で判断します．この値が大きければ，順次，目的変数群と説明変数群で正準負荷量（構成概念との相関係数）が大きい変数を確認します．仮に，身長，体重の順に正準負荷量が高く，握力，背筋力の順に正準負荷量が高ければ，身長，体重の構成概念（体格）と，握力，背筋力の構成概念（力）の関わり合いが大きいといえます（意味づけは解析者の主観に委ねられます）．

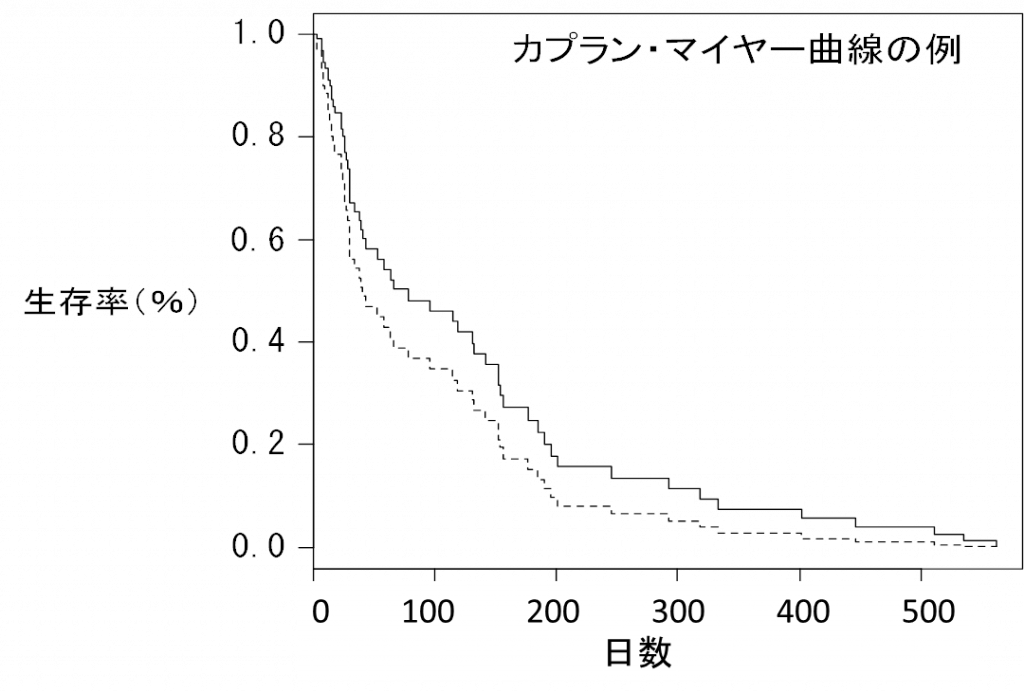
生存分析　survival analysis

イベントが｛起きる，起きない｝ということに対して，影響する要因を調べるのが生存分析です．生存分析の対象となるイベントの例として｛生，死｝，｛転倒あり，転倒なし｝，｛歩行可能，歩行不可能｝などの事象があげられ，｛生，死｝の場合は死，｛転倒あり，転倒なし｝の場合は転倒あり，｛歩行可能，歩行不可能｝の場合は歩行不可能をイベント発生として，治療の有無や入院歴の有無などの要因をもつことによりイベントの発生を時間的に早めるかどうかを解析します．代表的な手法にはカプラン・マイヤー曲線があり，検定手法の例ではログランク検定，多変量解析の例ではコックス・ハザード分析があります．

絶対リスク　absolute risk

絶対リスクとは，有害なイベントが発生する確率を意味します．リスク差と同義語です．ある介入の効果を検証する臨床研究では，介入群と対照群の絶対リスクをそれぞれ計算し比較します．その際，介入群の絶対リスクが対照群の絶対リスクより大きい場合は絶対リスク増加，小さい場合は絶対リスク低下と呼びます．介入によって有害なイベントが減少するのが望ましいことから，絶対リスク低下の場合，その介入は有効であるといえます．
たとえば，100人中10名の患者に有害なイベントが発生した場合，絶対リスクは10/100×100＝10％と表すことができます．

絶対リスク低下　absolute risk reduction

対照群の絶対リスクから介入群の絶対リスクを引いた値として表され，差が大きいほど研究で実施された介入の効果が大きいといえます．
たとえば， 糖尿病境界型と診断された方を対象として，対照群は栄養指導のみ，介入群は栄養指導に加えて定期的な運動を取り入れる介入とするランダム化比較試験（RCT）を考えてみると，結果として対照群の糖尿病発症率が7.5％，介入群の糖尿病発症率が5.3％であった場合，絶対リスク低下＝7.5％-5.3％＝2.2％となります．この研究では，定期的な運動を取り入れる介入によって，調査対象者全体の2.2％が糖尿病の発症を予防できたといえます．

説明変数（独立変数）　explanatory variable ( independent variable)

臨床研究において何らかの因果関係について検討する際に，ある要因によって結果に影響を及ぼすか，あるいは少なくとも結果と関連すると考えられる要因となる変数のことを説明変数あるいは独立変数といいます．たとえば，筋力や関節可動域，あるいは脚長が歩行速度に影響しているかどうかを検討する際には，歩行速度が目的変数（従属変数）で，筋力・関節可動域・脚長が歩行速度に対する説明変数（独立変数）ということになります．

線形混合モデル　liner mixed model（LMM）

　線形混合モデルは反復測定分散分析と似たような統計的手法で，複数の条件で反復測定されたデータに対して条件による平均の差を検定するときに適用できます．反復測定分散分析と異なる最大の特徴は，データの中に欠損値が含まれていても問題なく適用できる点です．反復測定分散分析は欠損値があると適用外となります．
　反復測定分散分析と同じように，整形外科疾患の術後患者10名を対象とした例をあげます．術後1週目・2週目・3週目の3つの時期に分けて，術後の膝伸展筋力が時期によって変化する（差がある）かどうかを調べたいとします．ここで， 1週目・2週目・3週目のすべての時期で対象者全10名の膝伸展筋力を測定できた場合には，反復測定分散分析と線形混合モデルのどちらを適用しても構いません．しかし，対象者Aさんがやむを得ない事情により2週目の測定を行えず，データに欠損値が生じてしまったとします．このような場合，もし反復測定分散分析を適用しようとするならば，Aさんのデータは除外しなければいけません．一方，線形混合モデルであれば2週目の測定値が欠損しているAさんのデータを含めたままで適用することができます．
　線形混合モデルは，一般化線形混合モデル（generalized linear mixed model；GLMM），混合効果モデル（mixed effect model），線形混合効果モデル（linear mixed effect model；LME）　，反復測定による混合効果モデル（mixed effect model for repeated measures；MMRM）と呼ばれることもあります．

尖度　kurtosis

データが正規分布しているかどうかを確認する指標の一つで，分布の形状が鋭い・平たいといった尖り具合を表す統計量です．統計ソフトによって出力された尖度（数値）が0のときに正規分布 しているとみなされます．ただし，尖度が3のときに正規分布とみなす方法もあり，解釈には注意が必要となります．

層化　stratification

　母集団から標本を抽出する方法は，大きく無作為抽出法と有意抽出法とに分けられます．無作為抽出法とは母集団からランダムに標本を抽出する方法で，有意抽出法とは母集団を反映するような標本を意図的に抽出する方法です．
　無作為抽出法の1つに層化抽出法（または層別抽出法）という方法があります．性別や年代，地域といった母集団の特性を考慮していくつかの部分集団（＝層）に分けることを層化（または層別）といいます．層化抽出法は層化によって母集団の特性をできるだけ保つように配慮して標本を抽出する方法で，小さなサンプルサイズでも推定精度を高めることができる利点があるとされています．層化抽出法の手順として，比例配分や最適配分，等配分といった方法に従います．
　比例配分は，母集団における各層の比率をもとにして，標本でも母集団と同じ比率で各層の人数を配分する方法です．たとえば，研究対象とする母集団で性別を層に分け，その割合が男性40％，女性60％であったとします．標本全体のサンプルサイズを100人と想定しているならば，男性40人，女性60人と配分してデータ測定を行うという手順になります．
　最適配分では，母集団での各層の比率のほかにデータのばらつきも考慮して，標本全体のばらつきが最小となるように配分します．おおざっぱな例となりますが，母集団の性別で男性90%，女性10％の比率だったとき，女性は人数が少ない分データのばらつきが大きくなる特性があるとします．サンプルサイズ100人と想定しているとき，ばらつきの小さい男性は母集団と比較して，やや少なめに70人，ばらつきの大きい女性はやや多めに30人と配分することで，ばらつきの大きさがなるべく均一になるように調整して標本を抽出します．
　等配分とは，各層の比率を同一にして標本を抽出する方法です．たとえば，サンプルサイズ100人であれば，性別の層を男性50人，女性50人と均等に配分します．

相関 correlation

　相関とは2つの変数の間の直線関係をみることです．
　2つの変数間で一方が大きくなると他方も大きくなる正の相関，一方が大きくなると他方が小さくなる負の相関があり，相関の程度を示す指標として相関係数を用います．相関係数は１または－1に近づくほど2つの変数間の線形関係は大きいといえます．
　たとえば，立位体前屈と柔軟性（膝関節伸展位での股関節屈曲角度）の関係を見たいとき，パラメトリックな手法の場合はPearsonの相関係数，また，ノンパラメトリックな手法の場合はSpearmanの順位相関係数を求めます．

相対リスク　relative risk

介入群と対照群の有害イベント発生率[→イベントを参照]の比によって求められる相対的な指標です．リスク比と同義語です．対照群の有害イベント発生率を分母として割り算し，１のときは介入効果がない，１より小さいときは介入が有効，１より大きければ介入が有害であり，１より小さければ小さいほど介入効果が大きいことを表します．相対リスクの特徴として，発症率に依存しない，言い換えると介入群と対照群のベースラインの発生率に違いが見えてこないことがあります．そのため，相対リスクだけではなく，絶対リスクでも評価することが推奨されています．また，後ろ向き研究，メタ分析，ロジスティック回帰分析では，リスクを計算できないので，相対リスクをオッズ比で代用します．

相対リスク低下　relative risk reduction

相対リスク低下は，1から相対リスクを引いて求めることができます．0のときは治療効果がない，0より小さいときは介入が有害，0より大きければ介入が有効であり，0より大きければ大きいほど介入効果が大きいことを表します．
たとえば， 糖尿病境界型と診断された方を対象として，対照群は栄養指導のみ，介入群は栄養指導に加えて定期的な運動を取り入れる介入とするランダム化比較試験（RCT）を考えてみると，結果として対照群の糖尿病発症率が7.5％，介入群の糖尿病発症率が5.3％であった場合，相対リスク低下＝1-（5.3％/7.5％）＝0.29（29％）となります．この研究では，定期的な運動を取り入れる介入によって，対照群に対して介入群では糖尿病の発症率が29％減少したといえます．

Sympsonのパラドクス　Simpson's paradox

　複数の研究結果を統合する時に，サンプルサイズを考慮せず単純に値を合計して有効率を計算すると，実際の値と逆の結果となることがあります．
たとえば，A施設とB施設における触診の成功率について計算していきます．

施設Aと施設Bでは，どちらも初心者よりも熟練者の方が，成功率が高いです．これらのデータをもとに，成功数と失敗数を足し算して成功率を計算すると，熟練者の成功率が初心者よりも低くなり，現実との矛盾が生じます．

　複数の研究結果を正しく統合する方法として，サンプルサイズに影響を受けない指標である効果量を算出する統計学的手法である重みづけ平均を用いる必要があります．
 

選択的アウトカム報告バイアス　selective outcome reporting bias

　報告バイアスの1つで，コクランレビューのリスクオブバイアス(RoB)の6項目のうちの1つです．臨床試験では一般的に複数のアウトカムを報告しますが，研究者は有意差のあったものを強調することが多い傾向にあります．このように，研究者が解析やアウトカムを操作し，最もインパクトの強い結果に応じて選択的に情報を報告することを，選択的アウトカム報告バイアスといいます．ただし，レビュアが1次研究の著者に連絡し，結果が完全に開示されているという確証を得たことを報告している場合は，このバイアスの可能性は低いです．
 

Summary of Findings (SoF)

　システマティックレビューによって得られた知見の概要をアウトカムごとに一覧にした表を意味し，レビューの結果の概要をつかむことができます．Summary of findings （SoF）表は，①アウトカム，②想定リスク，③対応リスク，④相対効果，⑤参加者数，⑥エビデンスの質，⑦コメントの7項目から構成され，アウトカムごとに記載される点，エビデンスの質が記載される点が特徴となっています．通常はabstractのすぐ後にある水色の表（下表）として示され，コクランレビューにSoFが記載されていればチェックする必要があります．

侵襲　invasion

　研究目的で行われる，穿刺・切開・薬物投与・放射線照射・心的外傷に触れる質問等によって，研究対象者の身体又は精神に傷害又は負担を生じさせることです．短時間の表面筋電図・心電図の測定，超音波画像の撮像，短時間で回復するような運動負荷については“侵襲を伴わない”と判断されることもありますが，対象者の年齢，身体的・心理的状態，測定の実施頻度や環境などを総合的に考慮すると，絶対的に“侵襲を伴わない”とはいえない場合もあります．

サラミ出版／イマラス出版　salami publication（salami slicing）／imaｌas publication

　研究業績量を膨らませるために，一つの研究を小分けに複数の論文に分割して報告する方法です．サラミ論文，分割出版とも呼ばれます．同様の目的で，これとは逆に同一の研究テーマであるにも関わらず，データを加えながら継続して発表する方法をイマラス出版といいます．イマラス出版とはsalamiの反対読み―imalas―に由来します．
　こうした発表方法は，個々の論文の質を低下させる危険性があります．明確な不正行為とはいえないグレーゾーンなのですが不適切な行為，好ましくない行為とされており，学術団体や研究組織によっては不正行為とみなされる場合もあります．
 

第Ⅰ種の過誤（αエラー）　type I error　（α error）

タイプIのエラー，アルファ（α）過誤とも呼びます．差の検定を例としてあげると，真（本当）は差がないデータの平均どうしで，「差がある」と誤って判定することを指します．一般に行われる検定では，有意水準（普通は5％）未満の第Ⅰ種の過誤（αエラー）が存在します．

対応のあるデータ paired data

同じ対象者に対して複数の条件下で測定を行い，得られたデータのことをいいます．たとえばA，B，Cという3人の被検者に対して，膝伸展筋力増強運動を行う前の膝伸展筋力と，行った後の膝伸展筋力のデータを，対応のあるデータと呼びます．測定条件が3つ以上の比較を行うために分散分析を行う際には，特に反復測定のデータ[反復測定分散分析を参照]と呼びます．

対応のないデータ　unpaired data

異なる集団の対象者どうしから得られたデータを，対応のないデータといいます．たとえば，健常群と患者群の握力データは対応のない2群のデータとなります．

第Ⅱ種の過誤（βエラー）　typeⅡerror　（β error）

タイプⅡのエラー，ベータ（β）過誤とも呼びます．差の検定を例としてあげると，真（本当）は差があるデータの平均どうしで，「差がない」と誤って判定することを指します．一般に行われる検定では第Ⅱ種の過誤（βエラー）は設定しないため，特殊な計算をしないと求めることができません．
nの数が多くなると検定力は大きくなり，第Ⅱ種の過誤（βエラー）は小さくなる性質があります．逆に，nが少なくなると検定力は小さくなり，第Ⅱ種の過誤（βエラー）は大きくなる性質があります．

代用エンドポイント　surrogate endpoint

代用エンドポイントとは，患者にとって重要である真のエンドポイントに関連するアウトカムのことをいいます．代用エンドポイントは，真のエンドポイントより臨床において測定しやすいこと，介入によって変化しやすいことなどから注目されることが多いです．しかし，代用エンドポイントがいくら改善または向上しても，真のエンドポイントが改善しなかったり，悪化したりすることもあります．
たとえば，転倒予防を目的としてバランストレーニングを行った結果，代用エンドポイントであるバランス能力は向上したが， 真のエンドポイントである転倒発生率には有意な減少が認められなかったなどがあげられます．

対立仮説　alternative hypothesis

帰無仮説に対立する仮説（H₁）です．反対（対立）の意味を持つ仮説なので，“差がある（差は0ではない）”，“関係がある（相関が0ではない）”などの意味を持つ仮説です．

多重共線性　multicollinearity

　重回帰分析やロジスティック回帰分析などの多変量解析を行ったときに，互いに関連性の高い説明変数（独立変数）が存在すると解析上の計算が不安定となり，回帰式の精度がきょくたんに悪くなったり，回帰係数やオッズ比などが異常な値をとったりする場合があります．このように解析結果が不安定な状態となる現象を多重共線性（またはマルチコ現象）といいます．
　多重共線性が起こりやすい条件として，①説明変数（独立変数）間の相関係数が±1に近い組み合わせが含まれること，②説明変数（独立変数）の個数がサンプルサイズに比べて大きいことなどがあげられます．いずれの条件に該当しても多重共線性が起こらない場合もあり得ますが，解析を行う前，あるいは解析結果を解釈する際にこれらの点に注意する必要があります．
　解析結果をみて異常な値が存在しないかどうかを見て，もし存在するのであればまずは説明変数（独立変数）間の相関係数を確認する必要があります．異常値が存在し，かつ強い相関を認める説明変数（独立変数）の組み合わせがあるようであれば，どちらか一方の説明変数（独立変数）を除外して再度解析を行わなければなりません．可能な限り，解析を行う前に明らかに相関が高い変数（たとえば，日常生活動作の評価尺度であるBarthel IndexとFIMの点数）の場合は，はじめからどちらか一方のみだけを説明変数（独立変数）にするようにします．
　サンプルサイズに関しては，説明変数（独立変数）の個数よりも十分に大きくなるよう，データ測定前に計画しておくことが望ましいでしょう．

多重比較法　multiple comparison procedure

3つ以上の群または変数のデータの差に対して検定するとき，2つずつの組み合わせでは検定の回数が多くなり，有意確率の値が高くなるという問題（多重比較の問題）が起こります．これを避けるために，繰り返す検定の数に応じて有意確率を調整する方法が多重比較法です．慣習的には，分散分析で有意差があった後に，どのデータとどのデータに差があるかを調べるために行う，その後の検定（post-hoc test）として利用されます．多重比較法には，Tukey法を始めとした，様々な手法が考案されており，それぞれで一長一短の性質があります．

脱落　dropout

　研究に参加する対象者の中には，治療方針の変更や研究途中での本人の拒否など何らかの事情で追跡不能になる場合があり，これを脱落（ドロップアウト）といいます．たとえば，新しい筋力トレーニングの効果を検証するためのランダム化比較試験（RCT）による比較研究において，介入群の対象者の一部がトレーニングに伴う苦痛や不快感のために脱落した場合，この脱落者を除外して効果を検証しても，そのトレーニング方法が現実的に妥当かどうかという問題があります．また，脱落者を含めて検証を行った場合とは結果が異なる可能性もあります．そのため，治療の現実性も含めて検証するためには，途中で脱落した人も最初に割り付けられた群に含めて解析することが重要であり，これを治療企図解析（ITT解析）といいます．

妥当性　validity

妥当性とは，その研究が目的としている事象を適確に捉えられているか，言い換えれば見たいものがきちんと見ることができているかということを指します．研究においては，バイアスによる誤差が少なければ，その研究は妥当性が高いといえます．また，研究そのものの妥当性は内的妥当性，その研究が一般集団，あるいは個人へ当てはまるかどうかの妥当性は外的妥当性と呼ばれています．内的妥当性は，研究デザイン，データの収集と解析などを批判的吟味しながら判断します．ランダム化比較試験（RCT）は，最も内的妥当性が高い臨床研究として有名ですが，研究の対象となる人が限定されることから，外的妥当性は低いとの指摘もあります．一方，全数調査をするようなコホート研究では，ランダム化比較試験（RCT）より外的妥当性は高いが内的妥当性は低いといわれています．
さらに，妥当性に関する用語として，ある測定が他の確立された基準尺度と関連しているかどうかを表す基準関連妥当性や個々の因子を組み合わせたときに測定項目全体が意図するものを測っているかどうかを表す構成概念妥当性などがあげられます．

Dunettの多重比較法　Dunett’s multiple Comparison procedure

　多重比較法のうちの1つの手法です．1つの対照群と2つ以上の処理群があるとき，対照群と処理群の比較のみを行いたいときに適用となります．たとえば，変形性膝関節症患者を対象として運動療法を施行しない対照群，運動療法A法を施行したA治療群，運動療法B法を施行したB治療群を設定し，対照群に対して運動療法を施行しているA治療群およびB治療群では膝関節痛の程度に差があるか検定するときに用いることができます．
　Dunettの多重比較法では対照群と処理群のみに注目しますが，処理群どうしの差も見たいならばTukeyの多重比較法かScheffeの多重比較法を使います．

多変量解析　multivariate analysis

3つ以上の変数間の複雑な関係を，同時に解析する方法です．重回帰分析，ロジスティック回帰分析，因子分析，正準相関分析，クラスター分析などがあります．例として，脳卒中患者の歩行速度に対して，ブルンストロームステージ，年齢，発症期間の3つの組み合わせがどのように影響するかを解析する重回帰分析があげられます．

治療企図解析（ITT解析）　intention to treat analysis

ランダム割り付けを行う介入研究において，研究を始める前に決定した対照群と介入群の割り付けを実験終了時にも変えずに解析する方法です．たとえば，対照群（被検者A，B，C）と治療群（被検者D，E，F）として研究を行い，研究を進めるうちに対照群の被検者Bが治療を受けたくなって治療群に変わったとか，治療群の被検者Dが治療を止めたというとき[→脱落を参照]でも，研究終了時の解析は当初の予定通り，対照群（被検者A，B，C）と治療群（被検者D，E，F）として解析する手法です．

治療必要数（NNT）　number needed to treat

ある介入を対象者に行った場合，1人に効果が現れるまでに何人に介入する必要があるのかを表す数字です．たとえば，治療Aを行ったときに，10％の有病率が5％に減少したとします．治療Bを行ったときに，50％の有病率が25％に減少したとします．これらの有病の減少率は何れも50％です．しかし絶対的な値をみると同じとは思えません．そこで，NNTという指標が生きてきます．NNTは1/（（介入前有病者数/全対象者数）－（介入後有病者数/全対象者数））で求めます．前述の例ですと，それぞれの実験で100人を対象としていたとすれば，治療AではNNT＝1/（10人/100人－5人/100人）＝20，治療BではNNT＝1/（50人/100人－25人/100人）＝4となります．治療Aでは20人に治療すれば1人に効果が現れるのに対し，治療Bでは4人に治療すれば1人に効果が現れるといえるので圧倒的に高い効果を得たことになります．

t検定（差の検定としての）t test

2つのデータの母集団が正規分布に従うとき，2つのデータの平均に差があるかを調べるパラメトリックな手法（パラメトリック検定）です．差の検定としてのt検定には，対応のないデータの差を調べる2標本t検定（two sample t test）と，対応のあるデータの差を調べる対応のあるt検定（paired t test）があります．
治療群と対照群（対応のないデータ）の平均握力に差があるかどうかを調べるときは2標本t検定を適用させます．A～Dの4名を対象として，介入前の片脚立位保持時間と介入後の片脚立位保持時間の平均値に差があるかどうかを調べるときは，対応のあるt検定を適用させます．

データの尺度　scale

データの尺度には比率尺度，間隔尺度，順序尺度，名義尺度の4つがあります．比率尺度とは，客観的な量として測られるデータのことです．このデータは原点（0）が決まっています．たとえば，長さ（cm），重さ（kg），時間（分）などがあげられます．間隔尺度とは，比率尺度と同じく客観的な量として測られるデータですが，0は決まっていない点が異なります．例としては知能評価尺度やADL評価尺度の得点などがあげられます．これらは0点であったとしても，知能が無（＝0）の状態，ADLが無（＝0）の状態であるとは限らないからです．
順序尺度とは，数値が大小関係のみを表すデータを指します．たとえば徒手筋力検査(0～5)やブルンストロームステージ(Ⅰ～Ⅵ)があります．ステージⅠとⅡの差の程度と，ステージⅢとⅣの差の程度は同じではなく，単にⅠよりⅡが悪い，ⅢよりⅣが悪いなどの解釈に留まります．
名義尺度とは，性別｛男，女｝や対象群｛A，B，C｝といった，属性により分類されるデータです．分類のみに意味があり順序には意味がありません．｛1＝A，2＝B，3＝C｝と数値を割り当てても，四則計算をすることはできません．なお，性別の男，女や，対象群A，B，Cの各グループを，カテゴリーと呼びます．

Tukeyの多重比較法　Tukey’s multiple comparison procedure

　多重比較法のうちの1つの手法です．多重比較法の中では最も適用範囲が広く，利用される機会が多い特徴があります．たとえば，若年群，壮年群，高齢群の3つの年代別に握力の差を比較したり，健常群，脳梗塞右麻痺群，脳梗塞左麻痺群の3群間で歩行速度を比較したりするといったときに用いることができます．

統計解析　statistical analysis

統計解析は，統計的解析，統計（的）手法，統計（的）方法など，様々な呼称がありますが，どれが正しい用語ということはなく，何れも用いられます．これらのうち，近年では「統計解析」を用いるようになってきています．
また，「統計処理」という用語も散見されますが，言葉の意味を考えても統計解析に代わる用語ではありません．
統計解析とは，統計学の理論に従い，統計をもとにして解析を行うことです．統計とは，集団の特性を客観的な数量（平均や中央値）で表すことであり，求められた数量を統計量といいます．統計量の計算の基となるものがデータです．
統計解析には，推定と統計的仮説検定があります．推定は，データから得られた推定量に対して，統計学の理論をもとにして母集団の様相を推測することを意味します．統計的仮説検定は，何らかの判断を行うために，両極端な仮説（差があると差がない，など）を設定し，統計学の理論を利用して仮説が受容できるかできないかを調べるものです．
たとえば，データの平均を求める，中央値を求める，95％信頼区間を求めるといったことから，重回帰分析を行って回帰式を求める，主成分分析を行って主成分負荷量を求める，などの手法は推定の範疇に入ります．2標本t検定，相関の検定，Tukey法による多重比較法を行って，有意確率を求め，何らかの判断（差があるとか，相関があるなど）を下すことを統計的仮説検定といいます．これらの解析全てをひっくるめて，統計解析と呼びます．

統計的仮説検定　statistical test of hypothesis

単に“検定”と呼ばれることが多いです．統計的仮説検定では，まず帰無仮説と対立仮説の2つを立てます．そして，自分のデータから得られる平均とか相関の状態が，どれくらいの確率で帰無仮説に合致するか，統計学的計算を用いて調べます．統計ソフトを用いると，検定ごとの帰無仮説に合致する有意確率p値が求まります．このp値が非常に小さいとき（一般的にp<0.05のとき），帰無仮説の状況は考え難いと判断して，対立仮説を採用します．
逆にp≧0.05の時は，帰無仮説を保留します．

等分散性の検定　test for equality of variance

　2群以上のデータに対して，それらの母集団のバラツキ（母分散）が等しいか等しくないかを検定する手法です．等分散性の検定として，F検定，Bartlett検定，Hartley検定，Levene検定などがあります．
　2標本t検定[→ｔ検定（差の検定としての）を参照]などの，等分散性が前提となる検定の事前検定として良く用いられます．そして，等分散性が保留される場合は2標本ｔ検定，当分散性が棄却される場合はウェルチの検定が適用となります．
　なお，等分散性の検定を行ってパラメトリックな手法か，ノンパラメトリックな手法かを選択する方法は間違いとなります．また，事前検定として等分散性の検定を行うという段階的な検定を繰り返す手続きは，検定の多重性の問題があるという意見もあります．

特異度　specificity

ある疾患を持たない人のうち，検査で陰性と正しく判定される割合です．たとえば，長谷川式簡易知能評価スケール（HDS-R）が20点以上で認知症ではないという基準を仮定したとき，対象者100人中90人が20点以上でかつ,確定診断として真に認知症でなかったとき，HDS-Rの特異度は90％となります．特異度が高いということは，「陰性の者を陰性と正しく判定する可能性が高い」ということになります．

度数分布　frequency distribution

集団から得られたデータを，整理して表された分布のことをいいます．通常，いくつかの階級に分けて順に区分（階級）化し，その区分に属するデータの個数を表示する表（度数分布表）で示します．

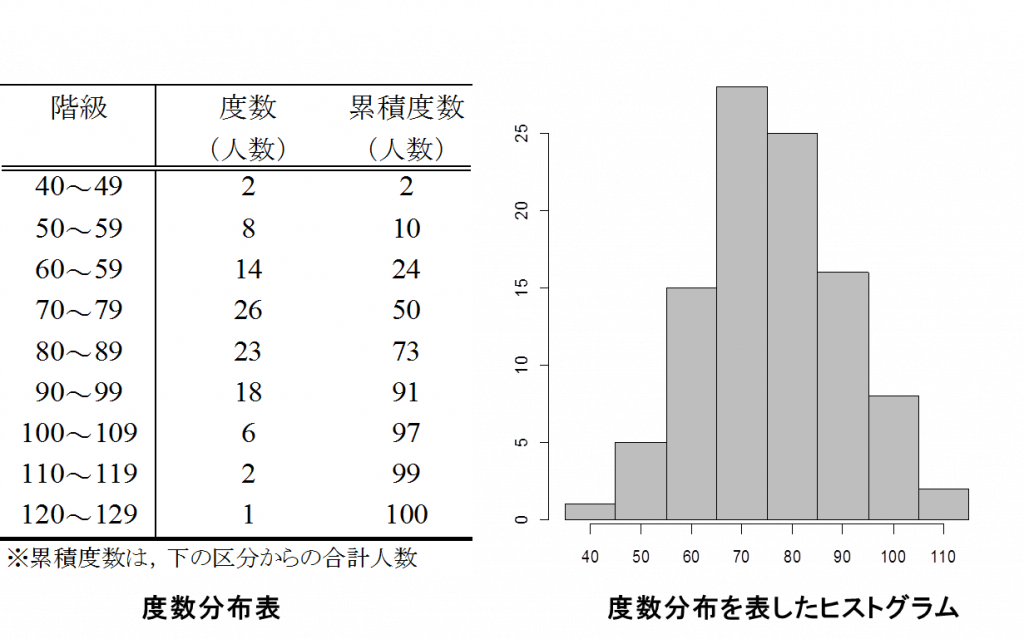
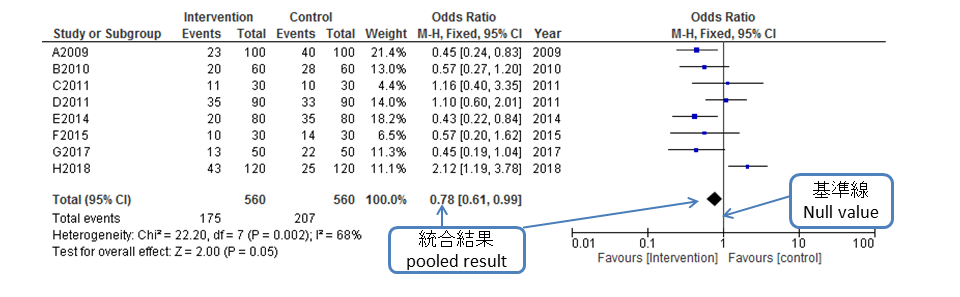
統合結果　pooled result

　複数の原著論文のデータをまとめて解析するメタ分析の結果のことで，フォレストプロットの◇で表されます．この◇は，中心が点推定値を，幅が95％信頼区間を表しており，中央の軸をまたいでいなければ有意差があることを示しています．統合結果は，統合推定値（pooled estimate）と示されることもあります．なお，統合結果は，異質性の検定を行った結果と合わせて確認する必要があります．
 

調整済み残差　adjusted standardized residual

　カイ2乗検定（χ2検定）を行ったときに，出力される調整済み残差をみれば各セルにおける人数（頻度）の多い少ないという程度を客観的に述べることができます．正確には“標準化された調整済み残差”といいます．調整済み残差が－1.96以下の場合は有意に人数が少ないセルであり，1.96以上であれば有意に頻度が多いことを示します．

ダミー変数　dummy variable

　名義尺度（データの尺度）のような数値の連続性を持たない2値分類データを0 と1に置き換えて数量化した変数のことです．性別は｛男性，女性｝の名義尺度ですが，これを男性＝0,女性＝1に置き換えるとダミー変数となります．さらに，年齢を3つに分類したデータ｛30歳代，50歳代，70歳代｝では，0-1の2つのデータ列を設けて，例えば30歳代は｛1列目＝1，2列目＝0｝，50歳代は｛1列目＝0，2列目＝1｝，70歳代は｛1列目＝0，2列目＝0｝と入力します．なお，2列の0，1の組み合わせで分類を区別さえできればよく，年代の順序は問いません．

Dersimonian-Laird法　DerSimonian-Laird mehod

　Dersimonian-Laird法はメタ分析における複数の原著論文のデータを定量的に結合させる統計的方法のうち，変量効果モデル（メタ分析）を用いて統合した効果量を推定する手法です．Dersimonian-Laird法は異質性の検定により複数原著論文の効果量間に明らかな異質性が認められる場合に適用されると考えられます．
 

盗用　plagiarism

　盗用とは，他人の研究方法，結果，文章（考察）などを，当該研究者の了解を得るかまたは適切に引用せずに自らのものであるかのように装うことをいいます．また，自分が過去に公表した文章を，新たな文章に再使用することは自己盗用と呼ばれます．盗用は　剽窃，盗作とも呼ばれ，捏造，改ざんと並ぶ研究における不正行為の1つです．剽窃と異なるのは，他人の内容を，ほぼそのまま流用する点です．
　盗用を避けるためには，適切な引用手段を満たさなければなりません．盗用は研究者倫理に反し，研究助成の差し止め，研究助成申請の禁止，その他の行政的・学術的・刑法的・民事的処罰が課せられます．

盗作　plagiarism

　他者が独自に著作物として表現した，独創的なアイディアを無断で使用し，自分の考えたものとして著作物を通して発表する全般的な不正行為のことをいいます．盗用，剽窃と類似していますが，盗作は特に文芸作品や芸術などの分野で用いられます．学術関連では，どちらかというと盗用が多く使われます．

種まき試験　seeding trial

　効果があると見込まれる機器や薬剤を使用して，その効果を確かめようと臨床試験を行うときに，研究成果そのものというよりは，その機器や薬剤の販売増加を期待していた場合，種まき試験の疑いが起こります．
　企業の考えた機器（種）を各研究施設に購入してもらい（蒔いて），研究に使用してもらい（試験），かつ効果が認められたら，もっと購入してもらえるという，対象者よりは企業にとって利益となる疑いが強い臨床研究を指します．
　種まき試験の定義は極めて難しく，種まき試験のように見えて全く問題のない研究もあります．種まき試験の疑いがかかる要点として，①既製品の効果をみている，②オープン試験である（マスク化されないPROBE法などをうまく使う），③研究実施者が研究機関の所属というより圧倒的に多くの臨床現場の者である，があります．

中間因子　intermediate variable

　中間変数，媒介変数とも呼ばれます．中間因子の性質は交絡因子とよく似ています．原因変数と結果変数の因果関係の過程で，時間的に中間に位置する変数のことです．
　中間因子は『条件①：原因変数の結果』となり，かつ『条件②：結果変数の原因』という2条件を満たします．中間因子と交絡因子についてパス図で表してみます．

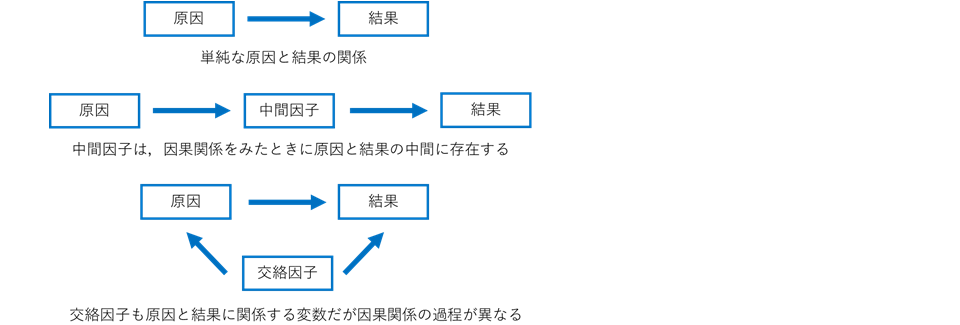
  　下肢の筋肉量（原因変数）と歩行速度（結果変数）の関係をみたいとき，膝伸展筋力も測定していたとします．このとき“膝伸展筋力”は①下肢筋肉量の結果であるし，②歩行速度の原因なので，中間因子となります．中間因子は，原因変数と同時に統計解析に含めない方が望ましい変数です．
　例えば下肢筋肉量と膝伸展筋力を説明変数（独立変数），歩行速度を目的変数（従属変数）とした重回帰分析を適用するのではなく，何れか1つの変数で回帰分析 した方が望ましいのです．

ナラティブレビュー　narrative review

　「ナラティブ」とは，患者が語る罹患の経緯，病気に対する考えなどの「物語」を通じて，病気の背景や人間関係を理解することを指します．ナラティブレビューは，システマティックレビューのようにバイアスを最小限にするための手法を用いずに書かれた総説のことで，書籍の中に典型的にみられるもので，疾患の原因，診断，予後または管理の1つまたは複数の局面に関わる考察が含まれ，多くの背景疑問，前景疑問および倫理的疑問が扱われています．レビューの著者は，クリニカルクエスチョンを挙げる際，滅多に報告されない疑問かいくつかの一般的疑問についての検討を行っていることが一般的で，1次研究論文を選択する際には滅多に報告されない研究サンプルか，報告されていてもバイアスがかかった研究サンプルを選択することもあります．さらに1次研究結果の質的評価や要約については滅多に報告されないか，報告されていても系統的でない場合が多いという特徴があります．しかし，自身が担当している疾患に対して疑問がある場合，その臨床病態に関する大まかな概要を得るために役立つレビューが，ナラティブレビューです．

2元配置分散分析　two-way analysis of variance（two-way ANOVA）

　1元配置分散分析は，1つの要因に対して差があるかどうかを検定しますが，2元配置分散分析は，2つの要因に関する平均の差を検定する手法です．たとえば，12人の対象者の握力を測るとして，「性別」の要因｛男，女｝の2群に差があるか，また「年代」の要因｛60歳代，70歳代，80歳代｝の3群に差があるかを知りたい場合，2つの要因が存在します．これらの各要因の群間で差があるかを検定する手法です．なお，各要因とも2群以上に分かれていれば，2元配置分散分析の適用となります．



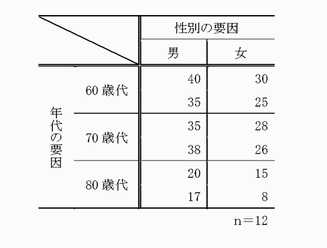
  　2元配置分散分析では，主効果と交互作用が有意性の判断の基準になります．もし，性別の要因で有意な差が認められた場合は，「性別の要因には有意な主効果が認められた」といいます．また，年代の要因で有意な差が認められなかった場合は，「年代の要因では主効果は認められなかった」といいます．さらに性別と年代の交互作用に有意な差が認められた場合は，「性別と年代の要因間で有意な交互作用を認めた」などといいます．

二次資料　secondary source

一次資料のデータを分析して得られた論文のことを二次資料といいます．臨床の現場では，数多くのエビデンスを検索・検証することはとても困難です．二次資料は，検証プロセスや評価基準が明記されており，より信頼性が高いといわれています．一般的なエビデンスの検索手順としては，クリニカルクエスチョンをPICOの形式に定式化し，次に情報源の検索を実行します．そして，選択されたエビデンスの検証すなわち批判的吟味を行い，それを担当患者に適用するかどうかの吟味を行うという流れがあります．しかし，情報源の選択時に，すでにエビデンスが精選されている二次資料を利用した場合は，エビデンスの批判的吟味という手順をスキップできることから，多忙な臨床現場でEBPTを実践するうえで効率的です．このように二次資料を有効に活用することで，より良い医療を効率よく提供することが可能となります．二次資料は，PEDroなどのエビデンスデータベースで検索することができます．

ノンパラメトリックな手法（ノンパラメトリック検定）　nonparametric method

母集団の分布がどのような場合でもできる検定手法全般をいいます．正規分布に従うデータに対しても適用できますが，基本的には比率・間隔尺度[→データの尺度]のデータのうち，正規分布に従わないデータや，順序尺度または名義尺度[→データの尺度]のデータに対して行われる検定手法のことです．
Wilcoxonの符号順位検定，Mann–WhitneyのU検定，カイ2乗検定（χ²検定）などが例としてあげられます．

ノンパラメトリックな手法の多重比較法 nonparametric multiple comparison procedure

　多重比較法として代表的なTukeyの多重比較法は対象となるデータが正規分布に従うことを前提としますが，データが正規分布に従わないときにはノンパラメトリックな手法の多重比較法を適用します．
　3群以上の差の検定を行うためのノンパラメトリックな手法の多重比較法として，Steel-Dwassの多重比較法があります．
　また，3群以上の比較の際に，2群ごとにMann–WhitneyのU検定を適用するとか，3条件以上の比較の際に2条件ごとにWilcoxonの符号順位検定を適用して，Bonferroniの調整を行う場合も，ノンパラメトリックな手法の多重比較法となります．

ネットワークメタ分析　network meta-analysis

　3種類以上の治療法の結果を統合するメタ分析で，ネットワークメタ分析，あるいはmultiple treatment comparisonなどと呼ばれます．従来のメタ分析では2種類の治療法を直接比較することしかできませんでしたが，直接比較と間接比較の統合解析によって過去に直接比較していない治療法も含めて，どの治療法がもっとも優れているかなどを互いに比較可能となります．
　たとえば研究1（A vs B）と研究2（B vs C）から，A vs Cという間接的な比較を可能にします．ただし，研究はすべての治療の相対効果において同質である（異質性がない）ことが前提です．
 

捏造 fabrication

　捏造とは，一部または全ての存在しない研究結果を，全て実施したかのように偽造作成し，論文・学会発表する行為です．臨床現場や実験室で実際には測定・計測をしていないのに，何らかの作業によって実施したかのように意図的にデータを作成し，論文に使用する行為になります．
　盗作，改ざんと併せて研究不正行為の一つであり，研究者倫理に反するため，研究助成の差し止め，研究助成申請の禁止，その他の行政的・学術的・刑法的・民事的処罰が課せられます．

二重投稿　duplicate submission

　同一の研究結果についての論文等（投稿中のもの，受理されたものを含む）を2つ以上の審査機関・出版社等に投稿することを二重投稿といいます．
　日本語で既に掲載された論文を英語に翻訳して投稿すること，またはその逆も二重投稿となり得ます．研究対象や方法，結果およびその解釈がすでに発表された論文や投稿中の論文と同一あるいは類似している場合や，図表やデータを適切な引用をせず，原著論文の一部とし投稿することも二重投稿に相当します．
　他誌で受理されなかった研究論文や，学会発表のために作成した抄録を改めてまとめた論文は二重投稿に該当しません．また，学士論文・修士論文・博士論文等を本格公表する論文として推敲・作成し直し，投稿することは許容されることが多いようです．
　ただし，投稿した審査機関・出版社等が，類似した論文が他誌に掲載されている事実を周知した上で，掲載が有益であると判断した場合は，編集者間の合意により受け付ける場合もあります．

バイアス　bias

バイアスとは，明らかにしたい真の結果を誤らせる要因のことであり，日本語では「偏り」や「誤差」と訳されています．バイアスの種類には，選択バイアス，情報バイアス，交絡バイアスの３つがあり，対象の選択，データの収集，結果の分析などで起こりやすいとされています．選択バイアスは，母集団から対象を選ぶときと，実験的研究であれば群を割り付けるときに生じる場合があります．選択バイアスを少なくする研究デザインとしてランダム化比較試験（RCT）があります．情報バイアスは，調査や測定によってデータを収集するときに生じるバイアスです．情報バイアスを少なくするためには，対象者，治療者，評価者に研究の情報を伏せる盲検法（ブラインディング）という手法がよく使われます． 交絡バイアスは，原因と結果を検証する際に，その背後に隠れて存在する交絡因子が存在することをいいます．交絡バイアスを少なくするには，ランダム化比較試験（RCT），マッチング，多変量解析，治療企図解析（ITT解析）が有効です．

箱ひげ図　　box and whisker plots

データの分布を「箱」と，上下に伸びる「ひげ」で表す図です．箱の中に引かれた横線は，中央値（50％値）を表します[→四分位数を参照]．箱の上辺は第1四分位数（25％値），箱の下辺は第3四分位数（75％値）を表します．ひげは，上辺と下辺からそれぞれ上下に2本，第1四分位数と第3四分位数の差（箱の長さ）の1.5倍離れた値以内で，1.5倍離れた値に最も近いデータまで伸ばします．それよりも離れた値を外れ値とします．

外れ値　outlier

　データが極端に大きいまたは小さいデータであり，かつ少数のデータのことを外れ値と呼びます．外れ値は統計解析を行う上で大きく影響することもあり，解析から除外した方が良いという考えがありました．
　外れ値を除外する代表的な検定として，グラブス・スミルノフ（Grubbs Smirnov）の検定があります．しかし，これは正規分布を仮定したときに異常と思われるものを外す検定であるため，多くの場合非対称な分布に従う医学的データにとって，正規分布に従うことを証明しない限りは，その測定値自体を異常と判断し，棄却してよいわけではありません．よって現状では，検定によって機械的に外れ値を外すということは推奨されません．
　外れ値を検出した場合は，計測上のミスがないかを確認し，可能であれば再計測を行う，外れ値を含めた考察と除外したことによる影響を検討する，正規分布を前提としないノンパラメトリックな手法（ノンパラメトリック検定）を用いて解析を行うなどの対応をとることが妥当です．また，報告の際には，外れ値を含む結果である，または外れ値を除外した結果である，というように，いずれの場合も明記する必要があります．

パラメトリックな手法（パラメトリック検定）parametric method

母集団が正規分布に従うデータに対して適用される検定手法全般をいいます．平均と分散（標準偏差の2乗）を用いて計算するのが特徴です．たとえば，差の検定（主にt検定）や，分散分析などがあげられます．数理的に性質が良く，信頼区間も求められる特徴を持ちます．

反復　replication

　フィッシャーの三原則の一つ．データを記録するときは可能な限り，2回以上の反復測定（繰り返し測定）を行うということです．1回のみの測定では，測定値に違いがあっても系統誤差なのか，それとも偶然誤差（たまたま生じる誤差）なのか（Bland-Altman分析を参照）は判断できません．「反復測定」によって，偶然誤差の大きさを評価することができます．
　例えばA，B，Cという比較したい条件が3つあり，1日に6回の測定までできるとします．その一つの例として，下に示すように3日間で各処理を6回ずつ行うことが考えられます．
 

1日目	2日目	3日目
AAAAAA	BBBBBB	CCCCCC

反復測定分散分析 repeated measure analysis of variance

　ある対象者群に対して，3条件以上の反復測定を行い，それらの平均の差を検定する方法が反復測定分散分析です．たとえば，整形外科疾患の術後患者10名を対象として，術後1週目の膝伸展筋力，2週目の膝伸展筋力，3週目の膝伸展筋力，…，と3つ以上の時期に分けて，術後の膝伸展筋力が変化する（差がある）かどうかを調べる場合に適用します．もしくは，健常人15名を対象として股関節回旋可動域を測定するとき，①背臥位で股関節90度屈曲位，②背臥位で股関節0度屈曲位，③端座位といった，3条件に変えて，回旋可動域がどう変化するかを調べる際にも，反復測定分散分析が適用されます．仮に，術後1週目の膝伸展筋力と2週目の膝伸展筋力だけの差，または，背臥位で股関節90度屈曲位と背臥位で股関節0度屈曲位だけといった2条件の差を調べたいときは，対応のあるt検定[→ｔ検定（差の検定としての）を参照]が適用となります．つまり「3条件以上の対応のあるt検定」と思ってもらえばイメージしやすいと思います．
　対象者は全ての条件に参加している必要があり，ある条件では別の対象者が入る，ということはありません．

Pearsonの相関係数　Pearson’s product moment correlation coefficient

Pearsonの相関係数は，2つの変数間の直線関係の程度を表すもので，パラメトリックな手法（パラメトリック検定）です．略語ではrと表記され，－1から1の範囲をとります．単に相関係数と呼ばれることもあります．
0から1の範囲にあるときは一方の変数が大きくなるに従い他方も大きくなるという正の関係が，－1から0の範囲にあるときは一方の変数が大きくなるに従い他方は小さくなるという負の関係があることを意味します．0のときは2つの変数が全く無関係で，1に近づくほど，または－1に近づくほど変数間の関係が強いことになります．

PICO

　EBPTの実践において適切な治療方針や根拠を導き出すためには，最初のステップとして，臨床的疑問（クリニカルクエスチョン）を，「①どのような患者に（Patient），②どのような評価・治療をしたら(Intervention)，③何と比較して(Comparison)，④どのような結果になるか(Outcome)？」という４つの要素に定式化し，文献検索を行いやすいように整理します．この定式化の手法は，４つの要素の頭文字をとってPICO，あるいはIをE（Exposure：暴露）に変えてPECOと呼ばれています．
　たとえば，2か月前よりテニスのバックハンドストローク時に右肘外側部に疼痛がある患者さんに対して，疼痛の軽減目的に超音波療法とマッサージのどちらが効果的かについて考えている場合には，P:慢性的なテニス肘の患者に対して，I:超音波療法を実施した場合と，C:マッサージを実施した場合で，O:疼痛軽減効果に違いがあるか？というふうに疑問を定式化します．
 

p値　p-value

p値は，有意確率，有意水準，危険率[→有意水準を参照]の表現として用いられます．統計解析では，検定の結果を表すもので，あらかじめ定めた有意水準と比較して判定します．

PPS解析　per protocol set

　ランダム化比較試験（RCT）において，計画どおりに治療を完了した被検者だけを対象に解析する方法です．一般的には治療が遵守されている，データの不足がない，重大なプロトコール違反がない，という最低限の規定を満たす被検者のみを対象とします．そのため，効果のある人だけが対象となったり，その逆として対照群との背景因子が異なってしまうなどの問題が発生しやすい欠点があります．

批判的吟味　critical appraisal

EBPTの5つのステップの一つには，「ステップ3　収集した情報（検索文献）の批判的吟味」があります．批判的吟味とは，入手したエビデンスの結果を鵜呑みにするのではなくバイアスを含んでいないかどうかを判断するための手続きのことを指します．一次資料の文献を批判的に吟味する場合のチェックポイントとしては，①研究デザインは適切であるか　（ランダム化比較試験（RCT）であるか），②比較した群間のベースラインは同様であるか，③盲検化[→盲検法（ブラインディング）を参照]されているか，④患者数は十分に多いか，⑤割り付け時の対象者の85％以上が介入効果の判定対象となっているか(脱落者が15％以内であるか)，⑥治療企図解析（ITT解析）がされているか，⑦統計解析は妥当であるか，⑧結果と考察との論理的整合性が認められるか，などの点があげられます．システマティックレビューなどの二次資料を入手した場合には，専門家によって内的妥当性[→妥当性を参照]が吟味されているため，ステップ3の文献の批判的吟味は行わず，ステップ4の患者への適用についての吟味に進みます．

標準誤差　standard error of the mean（SEM）

　データそのもののバラツキを表すのは標準偏差で，平均のバラツキを表すのが標準誤差です．平均のバラツキといわれても直感的には理解し難いはずです．なぜなら，標準誤差とは現実の値ではなく，理論的な推定値だからです．例を挙げると，変形性膝関節症患者10名の膝伸展筋力が平均15±2.0kgだったとします．標準誤差は，
　　
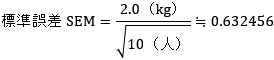
で計算されます．
　ここから推測の話です．上の例と同様に，たくさんの変形性膝関節症患者から10名の膝伸展筋力を測って平均を求める，という測定を∞人の研究者が行ったとします．求められた∞人分の平均は全員が同じ値になるとは限らないのでバラツキます．このバラツキ＝平均のバラツキ＝標準誤差というわけです．
　現実には標準誤差がどれくらいなら良いとか悪いとかという解釈はせずに，主に統計解析の計算に利用されるので，なじみの薄いものです．

標準偏回帰係数　standardized partial regression coefficient

　重回帰分析における説明変数（独立変数）の回帰係数は偏回帰係数と呼ばれます．例えば10ｍ歩行時間を目的変数（従属変数），年齢，体重，ファンクショナルリーチテストを説明変数（独立変数）とした重回帰式では，年齢の偏回帰係数は他の説明変数（独立変数）（体重，ファンクショナルリーチテスト）の影響を無視できるほどに小さくした，目的変数（従属変数）（10ｍ歩行時間）に対する偏回帰係数となります．
　全ての説明変数（独立変数）を平均0，分散1に標準化（変数の単位を統一化）した後，重回帰分析を行った場合の偏回帰係数が標準偏回帰係数です．標準偏回帰係数は各変数の単位に依存しない係数となるため，説明変数（独立変数）が目的変数（従属変数）に影響している度合いを比較できます．標準偏回帰係数は相関係数と同様の解釈で，－1から1の間の値をとり（まれに－1を下回ったり，1を超えることがあります．その時は－1または1とみなします），0は影響が無い状態で，－1ないしは1に近づくほど説明変数（独立変数）が目的変数（従属変数）へ及ぼす影響は大きいといえます．

標準偏差　standard deviation （sd）

標準偏差（sd）はデータの分布のばらつきをみる1つの尺度です．平均と標準偏差の値が分かれば，データがどの範囲にどのような割合で散らばっているか（分布） を推定することができます．データが正規分布しているという条件の場合，平均±sdの範囲には約70％，平均±2sdの範囲には約95％，平均±3sdの範囲には約99％のデータが入ることになります．

FAS解析　full analysis set

　治療企図解析（ITT解析）では，研究の途中で追跡不能となった者，研究参加を撤回した者などが発生しても全被検者を対象として解析する手法でした．
　しかし，現実的にはそのような例を無理してまで集めるというのは倫理上不可能な場合もあります．そこで，ランダム化比較試験（RCT）において全被検者から最小限の除外可能な被検者は除いて解析する方法がFAS解析です．たとえば適格性の条件を満たさない者，治療を一度も受けていない者，ランダム化後のデータが全くない者など，割り付けと関係のない理由に基づいて除外されます．ICH統計ガイドラインではこのような治療企図解析（ITT解析）の原則に可能な限り近づけた集団を，最大の解析対象集団とよび，FAS解析は広義の治療企図解析（ITT解析）に含まれると定義しています．

フォレストプロット　forest plot

　メタ分析の結果を図に表したもので，複数の研究結果とそれらを統合した結果を視覚的に確認することができます．フォレストは森林という意味であり，1つ1つの研究は木にたとえられています．□は個々の研究で報告されているアウトカムの点推定値（オッズ比，リスク比，平均値など）を，横棒の長さは95％信頼区間を示しています．なお，□の大きさは，サンプルサイズを表しており，サンプルサイズが大きく信頼区間が狭い研究が集まることで，統合結果を示す◇の信頼性が高くなるとされています．研究間の結果にばらつきがあるかどうかは，異質性の検定で確認することができます．◇の横幅は統合結果の95%信頼区間を示しており，アウトカムがオッズ比の場合，◇が１をまたいでいなければ有意差ありとなります．

ファンネルプロット　funnel plot

　システマティックレビューやメタ分析で，出版バイアスの有無を視覚的に判断するために用いられます．横軸は効果の大きさ（オッズ比や相対リスクなど）を，縦軸は精度（サンプルサイズや分散など）をプロットしていきます．出版バイアスがない場合には，左右対称にプロットされますが，効果が小さい側のプロットが少ない場合には出版バイアスがあることが考えられます．

フィッシャーの三原則　Fisher's three principles

　実験を行う際には実験計画を立てる必要があります．実験計画とは，よい結果を得るために最も効率的かつ効果的な実験を計画，その実験で得られたデータに対して最適な解析手法を採択する手順のことです．実験計画を立てずにやみくもに実験を行ってしまうと，費用や時間，労力を費やすだけではなく，信頼できる結果が得られない可能性もあります．
　そのため，R.A. Fisherがこの実験計画法の3原則を確立しました．この原則は以下の3点からなります．
・反復（replication）
・無作為化（randomization）
・局所管理（local control）

Bland-Altman分析　Bland-Altman analysis

　誤差には，系統誤差と偶然誤差があります．系統誤差とは，真の値に対して一定の偏った傾向を持った誤差（バイアスと同義）のことです．偶然誤差とは，真の値に対して大小ランダムに生じる誤差としてのバラツキです．偶然誤差は測定を繰り返すことによって平均が0に近づく性質がありますが，系統誤差は測定を繰り返しても，正あるいは負の方向に偏るため，誤った解釈を招くことになり，様々な方法で確認しなければなりません．
　系統誤差には固定誤差と比例誤差があります．固定誤差とは真の値に関わらず，特定方向に一定の幅で生じる乖離のことです．比例誤差とは真の値に比例して増減する，特定方向に生じる乖離のことです．
　Bland-Altman分析は，測定値に系統誤差が混入しているかを検討する手法の1つです．一対2つの測定値の差をy軸，2つの測定値の平均値をx軸にプロットした散布図（Bland-Altman plot）を作成し，それら測定値に含まれる系統誤差の有無・程度を可視的に確認する方法です．
　系統誤差が存在しない，つまり偶然誤差のみが存在する場合，下図のように，x軸から正負の方向にばらついた分布を示します．



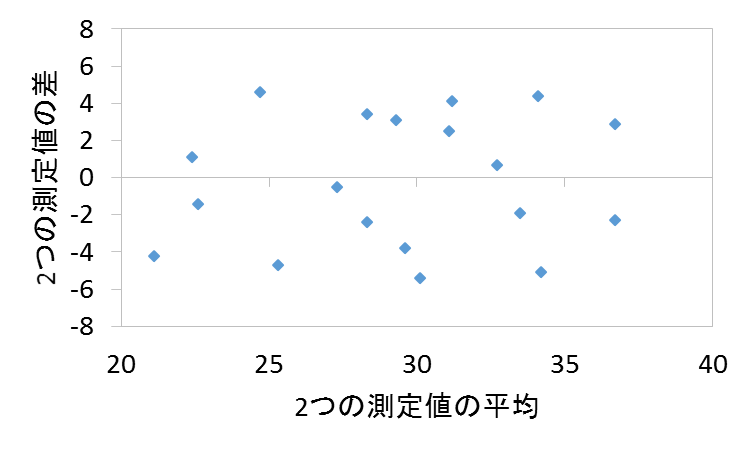
  　系統誤差のうち固定誤差が存在する場合，下図のように，x軸から正あるいは負の方向に偏った分布を示します．



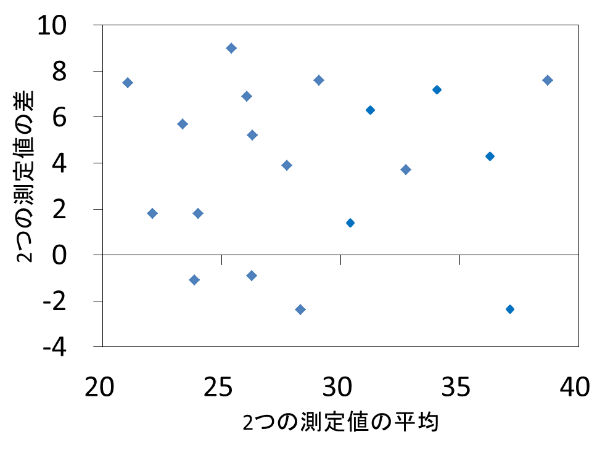
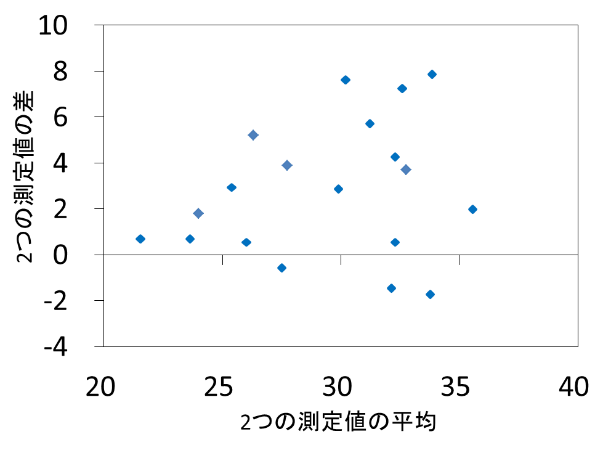
  　比例誤差が存在する場合，下図のように，横軸の値が増加するにつれて，2つの測定値の差の増加がみられる扇型の分布を示します． 

PRISMA声明　the Preferred Reporting Items for Systematic Reviews and Meta-analyses Statement

　システマティックレビューおよびメタ分析において，報告すべき項目が示されている声明を意味し，国際研究グループによって，1996年にメタアナリシスの質を向上させるために作成された「QUOROM声明」という指針を改訂することで，2009年に公表されました．この声明は，27項目のチェックリストおよび4段階のフローチャートで構成されており，文献検索の方法，検索で絞られた論文内容の統合，バイアスの報告，エビデンスの要約などを満たすプロセスが示されています．この声明は，システマティックレビューおよびメタアナリシスの国際的規範とも言えるものであり，私たちも，学術雑誌等にこれらを報告する場合には，この声明の原則に準拠することが求められています．
　ホームページ（http://www.prisma-statement.org/）にアクセスすると，チェックリストとフローチャートが英文でダウンロードできるようになっています．日本語に翻訳した内容は，卓ら^１） の文献を参照してください．
 

1. 卓　興鋼，吉田　佳督，他：エビデンスに基づく医療（EBM）の実践ガイドライン　システマティックレビューおよびメタアナリシスのための優先的報告項目（PRSMA声明）．情報管理．2011；54（5）：254-266．

Friedmanの検定　Friedman’s test

反復測定による（対応のある）分散分析[→対応のあるデータ，分散分析を参照]に相当するノンパラメトリックな手法（ノンパラメトリック検定）です．反復測定による分散分析とは，3変数以上の平均を比較し差があるかないかを検定する手法です．正規分布に従わず平均を指標とできない場合に，反復測定による分散分析の代わりとして用いられる検定です．
たとえば，運動療法の介入をした10名に対して，介入前，1ヵ月後，2ヵ月後，3ヵ月後と4回の時期に分けて膝伸展筋力を測定したとします．これらに差があるかという検定を行いたいとき，何れかの時期のデータが正規分布に従わない場合は，Friedmanの検定を適用します．それによって，これらの時期間の中央値に差があるかどうかを判断できます．

ブラウジング　browsing

　ブラウジングの意味は「草を食む（はむ）こと」に始まっています．「たくさんある草木の中から柔らかく食べやすいところを選んで食い取る」という意味として使われていました．ここから派生したブラウジングは，現在，「偶然」あるいは「目的を定めない」という探索方法全般を指す言葉として使用されるようになりました．本の流し読み，拾い読みなどがこれに当たります．臨床においては，自身が担当した疾患に対する治療法を調べる際，その疾患を対象とした雑誌を選び，目次を流し読みしながら（ブラウジングしながら）論文を読むことで情報を収集する方法が一般的ですが，これは効率的とは言えません．効率的良くブラウジングを行うには，対象とする雑誌を二次資料に限定して行うことが進められています．

プラセボ　placebo

　プラセボとは，臨床研究においては「偽薬」や「だまし薬」といった意味で使われます．例えば，疼痛に対する超音波治療の非温熱効果について調査する際に，一定の出力と時間で治療される介入群に対し，見かけ上は全く同じように設定して，出力オフで同時間実施される対照群を設定した場合に，対照群にも効果がみられたとします．このように実際には治療をしていなくても，治療に対する期待や満足度といった心理的な要因などからみられる治療効果のことをプラセボ効果といいます．

PROBE法　prospective randomized open blinded end-point study

情報バイアス[→バイアスを参照]をコントロールするために用いられる盲検法（ブラインディング）の一つであり，対象者が対照群と介入群のどちらに割り当てられているかという情報を，結果の評価者だけに伏せる方法です．
また，前向き研究であること，対象者を対照群と介入群へランダムに割り付けることも特徴としてあげられます．実際の臨床研究では，倫理的な観点からだけでなく，技術的にも対象者や治療者に情報を伏せることが難しいことがあるため，現実的な盲検化の手法であるPROBE法が注目されています．また，医学の分野では，対象者の心理面などの副次的効果もあり得るため，どの治療を行っているかを対象者に説明した上で効果を検証するのが妥当であるという理由でもPROBE法が用いられています．

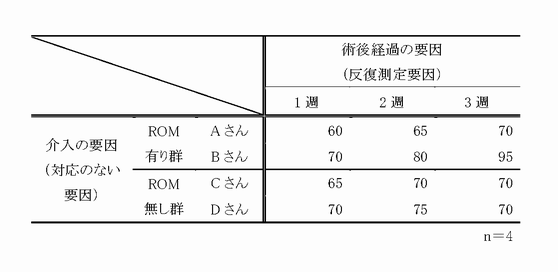
分割プロットデザインによる分散分析　analysis of variance for split-plot factorial design

　対応のない要因と，反復測定要因（対応のある要因）の2要因以上を組み合わせた差の検定を行いたいときに適用する分散分析です．対応のない要因とは，1元配置分散分析や2元配置分散分析と同じことになります．かたや反復測定要因に対しては，反復測定分散分析と同じことなります．これらを同時に検定したいときに，分割プロットデザインの分散分析を用います．
　ひとつの例として，対象者を人工膝関節全置換術後に介入の要因｛膝関節屈曲可動域運動を行った群，膝関節屈曲可動域運動を行わなかった群｝の2群（対応のない要因）で群分けし，さらに術後経過の要因｛術後1週，術後2週，術後3週｝の3変数（反復測定要因）で群分けした要因が存在するとします．これらの各要因の群間もしくは変数間で，平均に差があるかを検定する手法です．

文献レビュー　literature review

　文献レビューとは，あるテーマに関して既存の文献情報をもとにまとめた研究のことで，一定の手順と技術に基づいて実施され，それ自体が独立した研究方法論です．文献レビューを作成するときの論文構成は，一般の学術論文と変わりません．緒言，方法，結果（本論），考察と結論，引用文献リストの要素が含まれているのが一般的な内容です．文献レビューについては，様々な定義や方法論が論じられていますが，執筆の際には大きく分けて「網羅性（情報量）」と「独創性（新規性）」の2側面が要求され，独りよがりにならない論旨が求められます．網羅性・独創性ともに高い文献レビューほどシステマティックレビューに近くなり，独創性だけが高い文献はナラティブレビューに近くなります．システマティックレビューに近い文献レビューには，より時間と予算が必要となり，ナラティブレビューに近い文献レビューは，根拠が薄く思いが先行した文献レビューになる危険性を含みます．また，倫理面については，人を対象とした倫理的配慮が生じないのが一般的で，それゆえに文献レビュー研究が増えている背景も見られますが，著作権，盗用，剽窃などの倫理問題（出版・公表に関する倫理）は生じ得るので，筆者はこの点に対し注意することが必要です．

分散分析　analysis of variance

データの分散を利用して，平均の差の検定を行う手法です．主に，3つ以上の群または対応のあるデータに対して，平均の差を検定するときに利用します．
3群以上の対応のないデータに対して行われる平均差の検定として1元配置分散分析，3つ以上の対応のあるデータに対して行われる平均差の検定として反復測定による分散分析があります．分散分析の手法は多岐に及んでいて，2元配置分散分析，共分散分析，分割プロットによる分散分析などの複雑な手法も存在します．

分析的研究　analytical study

　研究デザインの枠組みで，現状のデータを記述する記述的研究に対して ，二つ以上の群を比較して分析する観察研究と人為的な介入を実施した実験的研究が相当します．分析的研究は，多くの場合には帰無仮説や対立仮説を立て，測定したデータを統計解析しながら自分が明らかにしたい因果関係や相関関係を理論的に証明することに適しています．

平均と中央値　mean and median

　平均と中央値はデータの中心的な値となる，データの代表値です．
　平均は，データの合計を対象数で割った値です．中央値は，データを小さいまたは大きい順に並べた時に中央（50％）に位置する値です．もし，データが偶数個ある場合は中心となる2つの値の平均を求めます．
　例題をあげましょう．5名の患者の年齢が57歳，59歳，64歳，68歳，77歳の時，平均は（57+59+64+68+77）/5＝65歳となり，中央値は大きさの順に並べた時に中央に位置する3番目のデータである64歳となります．
　比率尺度，間隔尺度のデータでヒストグラムを表した時に，およそ中心が盛り上がって左右均等に下がっていく正規分布に従うデータであれば平均，順序尺度や正規分布に従わない比率尺度，間隔尺度のデータであれば中央値を代表値として使用します．

ヘルシンキ宣言　Declaration of Helsinki

　ヒトを対象とする医学研究の倫理的原則について，1964年に採択された宣言のこと．
その内容は，数年ごとに修正されています．項目には，一般原則のほかに，リスク・負担・利益についてや，研究計画書について，研究倫理委員会について，プライバシーと秘密保持について，インフォームドコンセントについてなど，全部で12項目が記されています．

ベースライン　baseline

　研究を開始する時点における対象者の年齢，性別，疾患の重症度といった背景因子や臨床特性の状態・値の事をベースラインといいます．比較研究においては，研究開始の段階ですでに介入群と対照群のベースラインが同等でない場合，これらの特性が交絡因子となり研究結果に影響を及ぼす可能性があります．そのため,対象を選ぶ時点でマッチングを行ったり，割り付け方法を考慮することで，比較の対象となる群間におけるベースラインの類似性が確保されていることが重要になります．

PEDro　physiotherapy evidence database

PEDro（http://www.pedro.org.au/）は，インターネット上に公開された理学療法領域における文献データベースであり，ランダム化比較試験（RCT），システマティックレビュー，診療ガイドラインの情報を提供している二次資料です． PEDro に収録されたランダム化比較試験（RCT）は，最も有効な根拠に素早くアクセスできるように，PEDroスケールと呼ばれるチェックリストによりランク付けされています．11の評定項目のうち外的妥当性[→妥当性を参照]を判断する最初の項目を除いた10項目を満たすか否かを判定し，合計10点で評価されています．
PEDroは，CEBP（The Centre for Evidence-Based Physiotherapy）という組織が運営・維持しており，設立者は理学療法士のグループで，本拠地はシドニー大学ジョージ国際保健研究所に置かれています．PEDroの説明などについては，現在日本語バージョンで閲覧できるようになっています．

PEDroスケール　PEDro scale

PEDroに含まれているランダム化比較試験（RCT）の質を10項目で構成されるチェックリストを用いて2人の評価者によって点数で表されたものをいいます．内的妥当性[→妥当性を参照]としては，①ランダムに割り付けられているか，②隠蔽（コンシールメント）はされたか，③ベースラインが一致しているか，④評価者に盲検化[→盲検法（ブラインディング）を参照]はされたか，⑤対象者に盲検化はされたか，⑥治療者に盲検化はされたか，の6つがあり，統計学的情報の記載や方法としては，⑦対象者の85％以上にフォローアップが実施されているか（脱落者が15％以内か），⑧治療企図解析（ITT解析）がされているか，⑨統計学的群間比較の結果が報告されているか，⑩点推定値と信頼区間の両方を提示しているか，の4つがあります．また，外的妥当性[→妥当性を参照]は，項目としてはありますが，PEDro scaleの評価点数には含まれていません．

変数増減法（ステップワイズ法）　forward-backward stepwise selection method

　重回帰分析や多重ロジスティック回帰分析における説明変数（独立変数）を選択する方法として強制投入法，総当たり法，ステップワイズ法があります．変数増減法はステップワイズ法の一つで，有意な説明変数（独立変数）を1つずつ取り込んだり取り除いたりしながら，有意な回帰モデルを作成する方法です．なお，ステップワイズ法には，この他に変数増加法，変数減少法，変数減増法などといった方法もありますが，現在ではステップワイズ法と呼称するときは，Efroymson（1960）によって提唱されたこの変数増減法を指すのが主流となっています．
　統計解析ソフトでステップワイズ法を行うと変数が自動的に選択されるため，客観的かつ便利な方法です．しかし，いかなる統計解析でも共通なのですが，数理的な理論に基づいた説明変数（独立変数）が選択されるため万能ではなく，専門的な観点からは不要な変数が取り込まれたり，有意でなくとも必要な変数が除去されたりする危険性もあります．

変動係数　coefficient of variation(CV)

　標準偏差を平均で割って標準化し，百分率で表した値です．データの値が常に正の場合に適用できます．変動係数は単位が存在しない無数名であり，単位の異なるデータどうしで変動の程度を比較するときに用いられます．
　一般的には標準偏差をみてデータのばらつきを比べます．しかし，データの標準偏差が平均に比例して大きくなる特徴を持っている場合は，ばらつきの程度を標準偏差で比較せずに，変動係数を用いることで比較が可能となります．

母集団　population

　研究における対象は，標本（sample）と呼ばれ母集団から抽出された一部とされています．母集団は，実際に調査するのは不可能に近い無限大の大集団です．つまり研究では，母集団から抽出された標本に基づいて，母集団に関する結論を下しています．しかし，臨床的特性，各種の属性，時間的・地理的条件などが加わります．例えば，腰部脊柱管狭窄症に対する運動療法の効果の研究で，A病院の患者さんを対象として無作為に標本を選んだ場合，母集団はA病院の腰部脊柱管狭窄症患者さん全体となります．A病院の腰部脊柱管狭窄症患者さんの特性は70歳以上の者が多いとか，農作業に従事している人が多い，などの特徴がある場合，それが母集団の特性となります．通常は，広い範囲の腰部脊柱管狭窄症患者さん全体に一般化しようと考えるはずです．その，広い範囲の腰部脊柱管狭窄症患者さん全体という理想的な母集団を調査対象集団（universe）と呼びます．調査対象集団は母集団を包含し，母集団は標本を包含するという3段階で考えることにより，標本の母集団のバイアスを把握しやすくなります．
　なお，調査対象集団を目的母集団（target population），母集団を研究対象集団（accessible population）と呼ぶときもあります．

Bonferroniの調整（多重比較法）　Bonferroni correction

多重比較法の手続きの1つです．Bonferroniの方法などと呼ばれます．ある検定で得られた有意確率p値をBonferroniの補正によって修正すると，多重比較の問題[→多重比較法を参照]を避けることができるわけです．3群以上の比較にt検定（差の検定）を行うと，t検定を3回行わなければなりません．これでは検定の繰り返しという多重比較の問題が起こりますので，t検定で得られたp値をp×3（検定の繰り返し数）と補正して，補正後のp値がp<0.05となれば有意差ありと判断します．

ハダットスケール　Jadad scale

　ランダム化比較試験（RCT）の質を簡便に判断することができる評価ツールで，無作為化（０～２点），盲検化（０～２点），脱落（０～１点）の３つの項目が論文にどのように記載されているかを確認しながら点数をつけていきます．ランダム化比較試験（RCT）の質をさらに詳しく評価をする場合には，コンソート声明 のチェックリストで確認する方法があります．

フリー論文　free paper

　近年では，インターネットが普及し，世界中の論文にアクセスすることが可能になりましたが，有料で契約をしないと全文を読むことができない論文に対して，誰でも無料で全文を読むことができる論文のことをフリー論文と呼びます．
 

フォアグラウンドクエスチョン　foreground question

　調べて情報を得れば解決できるような学問的な疑問や教科書的な疑問のことをバックグラウンドクエスチョンと呼ぶのに対して，臨床現場での判断に関わる目の前の患者固有の問題をフォアグラウンドクエスチョンと呼びます．例として，「急性腰痛症のAさんに対して，どのように物理療法を実施するべきか」などが挙げられます．フォアグラウンドクエスチョンは，疑問が曖昧で漠然としてしまう場合が多いですが，ＰＩＣＯによって問題を定式化することで，問題の焦点が明確になります．
 

バックグラウンドクエスチョン　background　question

　臨床現場での判断に関わる目の前の患者固有の問題をフォアグラウンドクエスチョンというのに対し，調べて情報を得れば解決できるような学問的な疑問や教科書的な疑問のことをバックグラウンドクエスチョンと呼びます．例として，患者の疾患の病態についてや，実施しようとする治療法の一般的な効果などが挙げられます．

変量効果モデル（メタ分析）　random effect model

　メタ分析において，複数の原著論文の結果からオッズ比・リスク比などの効果量を統合するときに，原著論文間の効果量＝効果+研究間のバイアス+誤差と考えられるときに，変量効果モデルを使用します．Dersimonian-Laird法はこの変量効果モデルを仮定しています．
　かなりかみ砕いた簡単な例で説明すれば，複数の研究者が，ほぼ同質の対象に対して，同じ方法で，同じ評価法を用いた研究をしたと仮定します．しかし，それぞれの研究者の臨床環境は異なるとき，大なり小なり環境の違いが得られる効果に影響するはずです．そうした場合に，その効果を，環境の違い（研究間のバイアス）も含むと考慮して統合する方法が変量効果モデルです．

範囲制約性　bound constraint

　級内相関係数（ICC）は単に値が高ければよいとは限りません．なぜなら被検者の個人差（バラつき）によって値が変化するからです．被検者の個人差が大きいデータでは，検者の個人差や誤差が相対的に小さくなり，級内相関係数（ICC）が高くなります．
　例えば，握力測定の級内相関係数（ICC）を求めるとき，握力の強い人から弱い人まで幅広い対象にすれば，級内相関係数（ICC）を高くすることが可能です．これが級内相関係数（ICC）の範囲制約性の問題です．範囲制約性の問題を考慮するためには標準誤差（SEM）も求めて参考にします．
 

判別的中率　percentage of correct classification

　多重ロジスティック回帰分析における判別的中率とは，全対象者数に占める，実際の結果変数と解析結果（予測結果）の一致（正しく判別）した割合のことです．判別的中率＝（実際の結果と解析結果の一致した人数／全体の人数）×100（%）で求めます．判別的中率はいくつ以上あればよいという基準はありませんが, 高いほど有効な結果になっていると判断できます．

パス図　path diagram

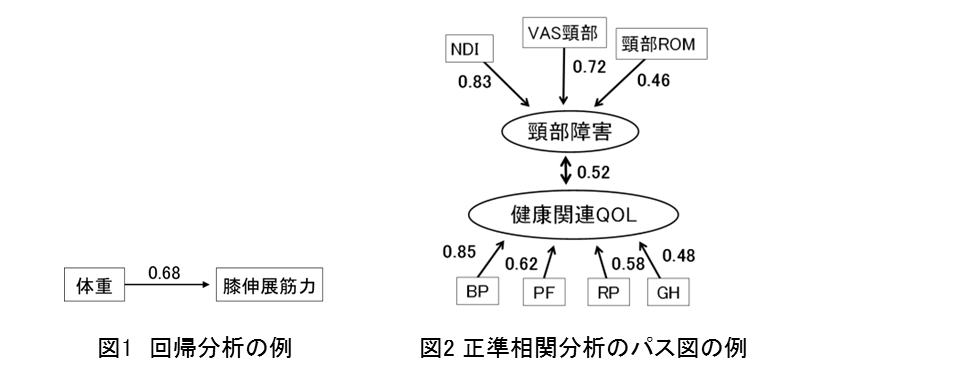
　パス図とは，変数間の因果関係や相関関係を矢印で結び，その関係性を図示したものです．実際に観測（測定）された変数は四角形で囲み，実際に観測されない構成概念は丸や楕円形で囲みます．変数間の因果関係は単方向の矢印（ → ）で，相関関係は双方向の矢印（⇔）で表します．この矢印の近くに，影響の大きさを表すパス係数を記載します．因果関係の場合は1つの例として標準偏回帰係数を，相関関係の場合は相関係数を記載します．
　例として回帰分析と正準相関分析の結果をパス図に示します．回帰分析（図1）では，膝伸展筋力（結果）に対して体重（原因）が影響したことを表しています．正準相関分析（図2）では，NDI，VAS，頚部ROMを主観的総合的に捉えて頸部障害（構成概念）と解釈し，BP，PF，RP，GHを主観的総合的に捉えて健康関連QOL（構成概念）と解釈した結果を表しています．頸部障害と健康関連QOLどうしは双方向の矢印で結んだ相関関係となっています．

Peto法　Peto method

　Peto法はメタ分析における固定効果モデル（メタ分析）を用いた方法の一つです．さらに，Peto法はランダム化比較試験（RCT）の統合に適した方法で，それ以外，例えば観察研究の統合には適していません．

Fisherの正確確率検定　Fisher's exact test

　2×2分割表の検定としてカイ2乗検定（χ2検定）がありますが，対象者数が少ない場合（正確には期待値が5未満のセルが全セルのうち20％以上存在する場合），カイ2乗検定の結果は不正確になります．この問題を避けるために，Fisherの正確確率検定で代用します．
　例えば過去1年の入院歴が｛あり，なし｝の分類と，過去1年の転倒歴｛あり，なし｝の関係で，人数を調査し，入院歴と転倒歴の関係を調べるとします．下表のように対象者数が小さい場合には，カイ2乗検定（χ2検定）ではなくFisherの正確確率検定が適用になります．

※表中数字は人数を表す．白文字数値部分の枠がセル（4つある）

最小の期待値の計算例：
最小の期待値＝1（行合計が最小の値）×10（列合計が最小の値）÷（総合計）25＝0.4
セル4つのうち1つが期待値0.4なので，少なくとも全セルの25％（4つのセルのうち1つ）が5未満である．

剽窃　plagiarism

　剽窃（ひょうせつ）とは，他人の研究方法，結果，文章（考察）などを，当該研究者の了解を得るかまたは適切に引用せずに部分的に加工して自らのものであるかのように装うことをいいます．盗用，盗作とも呼ばれ，捏造，改ざんと並ぶ研究における不正行為の1つです．盗用と異なるのは，部分的に加工する点です．
　剽窃は研究者倫理に反し，これが明らかになった場合，研究助成の差し止め，研究助成申請の禁止，その他の行政的・学術的・刑法的・民事的処罰が課せられます．

前向き研究　prospective study

一定の期間を経て前向きにデータをとる縦断研究の一つです．疾患の起こる可能性がある要因にさらされるかどうかに注目して群分けし，研究を開始してから将来（数ヵ月後，数年後）にわたって追跡を続け，疾病などの発生状況を比較する研究方法です．研究を開始する時点で，交絡因子などの影響を把握することができるといった利点がありますが，研究を終えるまで，かなりの時間と費用が必要となることが欠点としてあげられます．
ランダム化比較試験（RCT）やコホート研究などが代表的なものです．

孫引き　requotation

　孫引きとは，直接原典を引用するのではなく，他の論文誌や書籍に引用された文章をそのまま用いることを指します．論文で引用する文献は，必ず元論文を確認しなければなりません．論文や著書の中には，引用文献名や引用文の記載に誤りがあることが少なくなく，なかには元論文の主張のうち自己に都合のよい部分のみを恣意的に引用したり，さらには，元論文の趣意を変えて引用しているものもあることが指摘されています．論文を書く際，引用する部分について事実に対して少しでもあいまいな点があれば，必ず原典・元資料に当たることが求められます．元論文を確認しないでそのまま孫引きし，このことが後日発覚した場合には，論文の信頼性が大きく低下し，最悪の場合には責任問題も発生します．文献・図表の孫引き，無断引用は絶対にしないことが研究者として守るべき大事なことです．

マッチング　matching

ランダム化比較試験（RCT）や症例対照研究などの臨床研究において，対象を選択する時点で，背景因子となり得る年齢，性別，参加の動機付け，ならびにその他の臨床的特性などが，介入群と対照群ともに同等の割合となるように割り振ることです．マッチングをしたという記載がある研究では，結果の解釈を妨げる要因である交絡バイアス[→バイアスを参照]の影響をコントロールしようとしていることが分かります．

Mann–WhitneyのU検定　Mann–Whitney U test

対応のない2群のデータ[→対応のないデータを参照]に対して，分布の違い（2群の中央値の差）を検定するノンパラメトリックな手法（ノンパラメトリック検定）です．データの母集団分布はどのようなものであっても構いません．注意点は，サンプルサイズが2群間で同程度である必要があります．

無作為化　randomization

　フィッシャーの三原則の一つ．比較したい条件群を無作為（ランダム）に割り付けることです．実験の順序や場所が条件に影響を与えると思われる場合（系統誤差），無作為化によってその影響の偏りをできるだけ小さくすることができます．「無作為化」によって，系統誤差を偶然誤差に変換することもできます．
例えば，A，B，Cという比較したい条件が3つあり，1日に6回の測定までできるとします．単純にA，B，Cの順に繰り返すと，次のようになります（反復の例と同一）．
 

1日目	2日目	3日目
AAAAAA	BBBBBB	CCCCCC

　これだと，A，B，Cの条件差は，測定日による差が生じるかもしれません．そこで，次に示すようにA，B，Cの処理を行う順番を「無作為化」することが有効です．

1日目	2日目	3日目
CBABBC	BABCCA	ACCBAA

メタ分析　meta-analysis

統計的手法を用いてランダム化比較試験（RCT）など複数の原著論文のデータを定量的に結合させる総説論文のことを意味します．メタとは分析の分析という意味で，個々の原著論文の分析をまとめてさらに分析することを表します．システマティックレビューとは異なり，作成方法がエビデンスに基づいているか否かは問われませんが，結果のまとめ方に関しては定量的であることが必須となります．メタ分析の重要なポイントとして，各研究結果の均質性があげられます．結果に一貫性がなく，均質とはいえないメタ分析は要注意となります．
メタ分析の結果はオッズ比で表される場合が多いです．オッズ比とは１のとき効果なし，１より大きければ有害，１より小さければ有効という指標です．さらに，結果の表に示される横線がオッズ比を示す縦線と交わらなければ統計学的に有意であると言えます．真ん中の四角で示されたものが個々の研究のオッズ比を表しており，横線が信頼区間になっています．一番下に統合したメタ分析の結果がひし形で示されており，これがメタ分析によって求められた指標となります．

盲検法（ブラインディング）　blinding

データの収集や解析で起こりやすい情報バイアス[→バイアスを参照]をコントロールするために，対象者，治療者，結果の評価者，データの解析者へ情報を伏せる手法です．どのレベルで知らないかによって，一重盲検から四重盲検に分けられています．対象者だけに伏せれば一重盲検，対象者と治療者に伏せれば二重盲検となります．さらに，対象者と治療者だけでなく結果の評価者にも情報を伏せれば三重盲検，対象者と治療者と評価者だけでなくデータの解析者にも伏せれば四重盲検です．新薬の臨床試験では，プラセボ（偽薬）を使用した二重盲検がよく行われています．しかし，理学療法の研究では，厳密に盲検化できることが少ないのが現状です．そこで，注目されているのが，結果の評価者のみに情報を伏せる方法であるPROBE法です．

目的変数（従属変数）　object variable（dependent variable）

臨床研究において何らかの因果関係について検討する際に，ある要因によって影響された結果として表れる変数のことを目的変数あるいは従属変数といいます．すなわち，目的変数は説明変数（独立変数）に依存して定まると想定されます.
たとえば，筋力や関節可動域，あるいは脚長が歩行速度に影響しているかどうかを検討する際には，歩行速度が，筋力・関節可動域・脚長に対する目的変数（従属変数）ということになります．

メタ回帰分析　meta-regression analysis

　複数の研究論文の結果を，統計学的手法を用いて定量的に統合する分析をメタ分析といいます．しかし，現実には各研究での被験者の違い，研究デザインの違いなど，個別の要因の中でもある程度の差があります．それら複数の研究間で生じる差に影響する要因を探る方法をメタ回帰分析といいます．例えば，高齢者の歩行速度のメタ分析において，複数の研究論文で，対象が日本人または欧米人と人種が異なる可能性があります．また，高齢者の中でも70代，80代，90代と年代の異なる可能性もあります．メタ回帰分析は，これらの要因の影響をまとめて解析する手法です．

Mantel-Haenszel検定（法）　Mantel-Haenszel test（method）

　分割表の検定としてカイ2乗検定（χ2検定）があります．その複数の分割表を統合して総合的に検定する手法です．固定効果モデル（メタ分析）においてもよく用いられます．
　例えば分割表の検定として，転倒｛あり，なし｝と，過去の入院歴｛あり，なし｝の分割表を，年代｛60歳代・70歳代・80歳代・90歳代｝で層別化したとき，4つの年代別の分割表に対してカイ2乗検定（χ2検定）を4回行わねばなりません．Mantel-Haenszel検定ではこれらの4つのカイ2乗検定（χ2検定）を統合し，年代を調整したうえで検定することが可能です．
　また，Mantel-Haenszel検定（法）は固定効果モデル（メタ分析）を用いて統合した効果量を推定する手法でもあります．Mantel-Haenszel検定（法）は，異質性の検定により複数原著論文の効果量間に明らかな異質性が認められる場合，適用は難しくなります．
 

有意確率 probability

検定によって求められるp値のことです．統計的仮説検定では，これが有意水準と比較して大きいか小さいか評価し，判定することになります．

有意差　significant difference

差の検定を行って求めた有意確率p値が，定めた有意水準未満（一般にはp<0.05）となったときに，差があると判定する場合を，“有意差あり”といいます．逆に,有意水準以上になったときは,“有意差なし”といいます.ただし,“有意差あり”は,差の大きさを表すものではないので解釈には注意が必要です.

有意水準 significance level

帰無仮説を棄却する確率で，危険率ともいいます．第Ⅰ種の過誤（αエラー）を犯す確率ともなります．一般的に有意水準は5％が用いられますが，さらに厳しい1％が用いられるときもあります．
たとえば，差の検定を行ってp<0.05だった時は，差のない確率が小さ過ぎるゆえに，差がないとは考えられない，つまり差があると判定します．

尤度比　likelihood ratio

感度と特異度の比を表すもので，感度÷（1－特異度）で計算します．感度または特異度が高いほど，大きな値をとります．これは正確には陽性尤度比と呼ばれるもので，10より大きくなると有効な検査と判断できます．これとは反対に，陰性尤度比というものもあります．陰性尤度比は(1－感度)÷特異度で計算され，感度または特異度が高いほど，小さな値をとります．0.1よりも小さくなると有効な検査と判断できます．

有病割合　prevalence proportion

　疾患を有する可能性がある母集団のうち，実際に特定の疾患を有する者の数の割合のことです．研究や論文上において典型的な母集団となっているかを評価し，組み入れの結果として得られた有病割合と臨床現場の有病割合を比較し，批判的吟味を行う必要があります．

ラテン方格法　latin square design

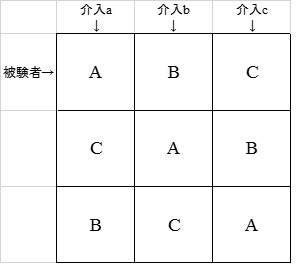
　ラテン方格を用いて割り付けを行う実験計画法のことを指します．たとえばn人の被験者にn種類の介入を行う実験をする場合，n行×n列の表を作り，行に被験者を，列に介入を行う順番を記入しておき，空いたマスに介入の種類を配列していきます．するとn種類の介入は次のようになります．①どの介入も1つの順序の中で1回実施されます．②どの被験者もすべての介入を1回経験します．　　　
　下図は3人の被験者（Aさん，Bさん，Cさん）に3種類の介入（a，b，c）を行う場合のラテン方格です．Aさん，Bさん，Cさんの3人全員が3種類の介入a，b，cを1回ずつ経験でき，配列に「釣り合い」がとれていることがわかります．また，これらの平均値は，順序効果に左右されないため，各被験者に平等の条件を与えることができるというメリットがあります．このようなn行×n列の表をラテン方格と言い，ラテン方格を用いることで介入や刺激の順序につり合いを持たせる計画法のことを，ラテン方格法と言います．

乱塊法　randomized block design

　もともとは農業分野から生まれた用語で，測定の反復（replication），無作為化（randomization），局所管理（local control），というフィッシャー(Ronald A.Fisher,1890-1962）の三原則を満たす研究デザインのことを乱塊法（Randomized block design）といいます．具体的には，実験の場を，測定環境（測定日・測定者・測定方法・対象者の背景因子や臨床特性など）が均一になるようにいくつかブロックに分けた上で，各ブロック内において比較する条件の順序を被験者ごとに無作為化することにより，比較される条件間の差の結果が偶然であることや，測定環境による影響を排除しようとするデザインのことです．
　たとえば，被験者90人に対し，3つの条件の異なる治療法（A.B.C）を割り当て，治療効果の違いについて検証する時，1日では時間が足りないため，実験実施日を3日間設定し，1日当たり30人の被験者に対して実験を行ったとします．この時，図のように実施日をブロックとし，各ブロック内に3つの条件の治療法（A.B.C）が同じ数（10回ずつ）になるように無作為に割り当てることで，実施日の測定環境による系統誤差を排除し，条件の違いによる治療効果の差を検証することが可能となります．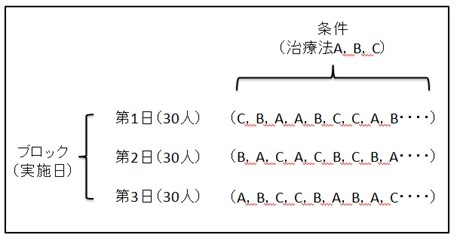

ランダム化比較試験（RCT）　randomized controlled trial

ある試験的操作（介入・治療など）を行うこと以外は公平になるように，対象の集団(特定の疾患患者など)を無作為に複数の群（介入群と対照群や，通常＋新治療を行う群と通常の治療のみの群など）に分け，その試験的操作の影響・効果を測定し，明らかにするための比較研究です．
群分けをランダムに行うのは，背景因子の偏り（交絡因子）をできるだけ小さくするためですが，コンピュータで乱数を発生させ，割り付け表を使用する方法が適切だとされています．くじ引きやサイコロの使用，患者番号などでの割り付けは準ランダム化となってしまい，真の意味でのランダム化とはなりません．
たとえば，脳卒中片麻痺患者を対象に，従来の運動療法と歩行練習のみを実施する群と，従来の運動療法に加えて免荷式トレッドミル歩行トレーニング（BWSTT）を追加して実施する群とにランダムに割り付け，BWSTTの効果を検討するといった研究デザインです．

利益相反　conflict of interest

　研究を遂行しようとする個人あるいはグループが，研究の方法や結果に昇進や報酬といった個人的利害を有していたり，研究に関わる他の人物や組織（スポンサーなど）との間に報酬や宣伝などの利害関係を有する場合には，それが研究の方法や結果に不適切な影響を及ぼす可能性があります．このような状況を利益相反が存在するといいます．
 

リサーチクエスチョン research question

リサーチクエスチョンとは，研究的疑問のことであり，クリニカルクエスチョンのうち倫理面や経済面などの条件を満たしたうえで臨床研究の対象となるものをいいます．クリニカルクエスチョンに関する先行研究をレビューし，わかっていることとわからないことを把握した上で，臨床的意義があり実現可能な条件を満たしたものがリサーチクエスチョンとなります．
たとえば，クリニカルクエスチョンとして，「P:慢性腰痛患者に対して，I:脊椎安定化トレーニングを行った場合と，C:行わなかった場合とで，O:脊椎の安定性に違いがあるか？」という疑問に対して先行研究をレビューすると，対象となる慢性腰痛患者の多様性や，介入案としてのトレーニング方法，アウトカムとしての脊椎の安定性の定義や定量化の方法，脊椎を安定させることの臨床的意義など様々な新たな疑問が出てきます．それらの疑問のうちで，上記の条件を満たし実現可能なものがリサーチクエスチョンになります．

両側検定　two-tailed test

　統計的仮説検定では，帰無仮説を設定しますが，対立仮説の状態によって両側検定，片側検定と呼び分けます．
　例を挙げて説明した方が理解しやすいと思います．例えば，A群とB群の平均の差の検定を行うとします．このとき帰無仮説は“平均Aと平均Bには差がない”と仮定します．統計的仮説検定を行って確率が小さいとき（p<0.05）は，この仮定が否定されますので，“差がある（対立仮説）”と判断します．しかし，“差がある”という内容には，“平均Aが大きく平均Bが小さいという差”と，“平均Bが大きく平均Aが小さいという差”の2種類が存在します．これらを併せて両側検定と呼びます．
　相関係数の検定でも同様です．“握力と体重に相関がない”と仮定して統計的仮説検定を行ったときに，p<0.05で否定されたとすると“握力が強くなるほど体重は重い”という相関関係と，“握力が強くなるほど体重は軽い”という相関関係の2種類が想像できます．これも両側検定です．回帰分析などでも同様です．ちなみに，差の検定で有意水準5％とするときは“平均Aが大きく平均Bが小さいという差”と，“平均Bが大きく平均Aが小さいという差”の2つを，それぞれp<0.025と設定するので，併せてp<0.05とします．
　もちろん，現実には平均Aが大きいとか，握力が強くなるほど体重は重い，という，何れかしか成立しません．しかし，理由はともかく現状では，原則として両側検定を使用する，という考え方が一般的です．

量的データ　quantitative data

アウトカム を表すデータの中で，温度や物の重さなどのように機器を使用して測定可能な連続データを量的データといいます．量的データはデータの間隔が一定であり，単位を有しています．データの尺度のうち，間隔尺度と比率尺度が量的データに含まれます．量的データが正規分布に従う場合には, パラメトリックな手法（パラメトリック検定)での統計的仮説検定に優れています．

臨床研究　clinical study

臨床研究とは，人間を対象とし，その目的が患者中心に立てられている研究のことで，リサーチクエスチョンについて立てた仮説を，実際の臨床で検証することを目的としています．臨床研究の中でも，特に前向き研究の中で研究者が治療法によって患者を割り付け，その有効性を検証するための介入研究のことを臨床試験といいます． EBPTの実践においては，ランダム化比較試験（RCT）など質の高い複数の臨床試験（一次資料）の結果をもとにメタ分析という方法によって統計学的に統合してまとめあげられたシステマティックレビュー（二次資料）の情報を臨床判断の材料として使用します．しかし，臨床試験の数が少なく二次資料が無い場合には，一次資料である原著論文を批判的に吟味[→批判的吟味を参照]しながら臨床判断の材料になるかどうかを検討します．網羅的に文献を検索したにも関わらず，二次資料も一次資料も無い場合には，自分自身の臨床研究によって新たなエビデンスを構築していくことが，わが国のEBPTの推進にとって重要な課題となります．

臨床判断　clinical decision making

臨床判断とは，理学療法の臨床活動において，評価や治療の方法などを選択することをいいます．従来の臨床判断は，教科書を参照しながら病態生理から類推して治療方針を作成したり，権威者の意見や先輩の指導，あるいは自分の経験則や得手不得手などに基づいて行われてきた傾向があると思います．しかし，このような臨床判断過程には，不確実性・偶然性・経験則によるバイアスによって，適切でない偏った臨床判断に至る可能性を含む場合があります．一方で，患者中心の医療を実践・提供することを目的とするEBPTでは，質の高い臨床試験の結果を科学的な根拠として臨床判断の材料としますが，それはあくまで一つの要素であり，基本的な理論や理学療法士の臨床能力，施設の設備・環境，そして，患者・家族の価値観や意向などの要素も統合することによって，目の前の患者にとって最も有益となる評価や治療方針に関する臨床判断を行うことが大切です．

Reporting Guideline

　研究の質を保証するために作成された指針です．研究デザイン別には，システマティックレビューおよびメタ分析に関してはPRISMA声明，ランダム化比較試験（RCT）に関してはコンソート声明，観察研究に関してはSTROBE声明，診断精度の研究に関してはSTRAD，症例報告に関してはCARE声明がそれぞれ示されており，能力低下やリハビリテーション分野の研究報告を掲載している28誌のリハビリテーション・ジャーナルはこれらの指針を積極的に使用することに合意しています^１）．研究者は，この指針に沿って作成されているチェックリストやフローチャートを研究計画の段階で確認することで，よりバイアスの少ない研究方法を検討することができかつ論文投稿時に必要な情報を知ることができます．

1. Leigton C,Allen W,et al: Elevating the Quality of Disability and Rehabilitation Research: Mandatory Use of the Reporting Guidelines．Phys Ther．2014；94：446-448.

ログ・ランク検定　log-rank test

　時間の経過の中で，あることが｛起こる・起こらない｝ということを調べるために，カプラン・マイヤー曲線を用います．しかし，これはグラフを見て主観的に判断するものなので，統計的検定を行って，差がある，差があるとはいえない，という判断が必要となります．
　その際に用いる代表的な検定法としてログ・ランク検定があります．ログ・ランク検定は，2群のカプラン・マイヤー曲線（生存曲線[→生存分析を参照]）に差があるかどうかを検定します．
　こうした生存曲線の差の検定は，ログ・ランク検定の他にもいくつか提案されており，一般化ウィルコクソン検定といった方法もよく見られます．

ロジスティック回帰分析　logistic regression analysis

2群で分けられた目的変数（従属変数）に対する，1つ以上の説明変数（独立変数）の影響を調べる統計解析の手法です．たとえば，歩行可能群と不可能群（2群で分けられた目的変数（従属変数））に対して，年齢，性別，握力，ADL評価得点など（4つの説明変数（独立変数））のうち，どの組み合わせが有意に影響するかを知ることができます．この手法の利点は，データの尺度や分布は，どのようなものであっても問わないという点です．
欠点は，目的変数（従属変数）が2群で分けられた場合しか解析できないという点です．

RevMan５　review manager 5

　メタ分析が実施できるフリーソフトReview Manager 5の略です．市販されている統計ソフトは高価であるため個人的に購入しにくいことがありますが，このソフトはコクラン共同計画のホームページから無料でダウンロードできるため，利用しやすいのが特徴です．複数の論文データを入力することで，フォレストプロットやファンネルプロットが作図できます．RevMan５は，英語のソフトであるため，使用する際には日本語で説明している解説本やインターネット上で公開されている説明文が参考になります．
 

リスクオブバイアス(RoB)　Risk of Bias

　コクラン・ハンドブックに掲載されているシステマティックレビューの具備条件の1つで，組み入れた論文の妥当性を評価したものです. 臨床試験においてバイアスは常に起きるので，バイアスが含まれているかもしれないリスクに注意をするという概念です．各アウトカムにおけるリスクオブバイアス(RoB)を論文ごと，項目ごとに示したものをRoBサマリー（下表）と呼びます．コクランレビューではリスクオブバイアス(RoB)を6つの領域（①適正な割付手順，②割付の隠蔽，③盲検化，④不完全なアウトカムデータへの対処，⑤選択的アウトカム報告バイアスの有無，⑥その他のバイアス）に整理して評価しています．評価結果は，緑・黄・赤の信号機の色でグラフに示されるため，これをみると個々の論文にどのようなリスクオブバイアス(RoB)が含まれるのかが視覚的にわかります．しかしこれはあくまで見やすく表示しているのであり，グラフから数値化することはできませんので注意してください ．

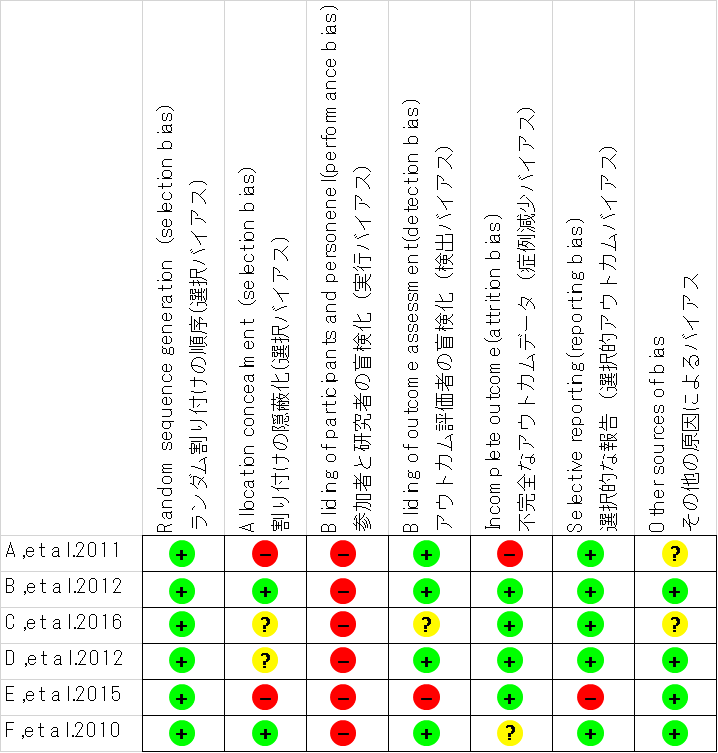
連関係数　coefficient of association

　分割表の行と列の関連度を表す指標で相関係数に似ています．カイ2乗検定（χ2検定）によりp<0.05で有意な偏りがあっても，何れかのセル（カテゴリー）で人数が多いか少ないという偏りを示すのみです．連関係数を用いることで行と列の人数の多いとか少ないという関連度を知ることができます．連関係数は-1～1の範囲をとり（種類によっては0～1），相関係数と同様に解釈します．様々な連関係数がありますが，2行2列の（2×2）分割表ではファイφ係数，それ以外の分割表ではクラメールのV係数などがあります．

歪度　skewness

データが正規分布しているかどうかを確認する指標の一つです．分布の形状が左右対称かどうかの歪み具合を表す統計量で，歪度が0のときに正規分布しているとみなされます．歪度が0よりも大きいときは左に偏った分布，0よりも小さいときは右に偏った分布であることを意味します．